大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問92 (数学Ⅱ・数学B(第3問) 問8)
問題文
問題を解答するにあたっては、必要に応じて 正規分布表(リンク) を用いてもよい。
ジャガイモを栽培し販売している会社に勤務する花子さんは、A地区とB地区で収穫されるジャガイモについて調べることになった。
(3)B地区で収穫され、出荷される予定のジャガイモ1個の重さは100gから300gの間に分布している。B地区で収穫され、出荷される予定のジャガイモ1個の重さを表す確率変数をXとするとき、Xは連続型確率変数であり、Xのとり得る値xの範囲は100≦x≦300である。
花子さんは、B地区で収穫され、出荷される予定のすべてのジャガイモのうち、重さが200g以上のものの割合を見積もりたいと考えた。そのために花子さんは、Xの確率密度関数f(x)として適当な関数を定め、それを用いて割合を見積もるという方針を立てた。
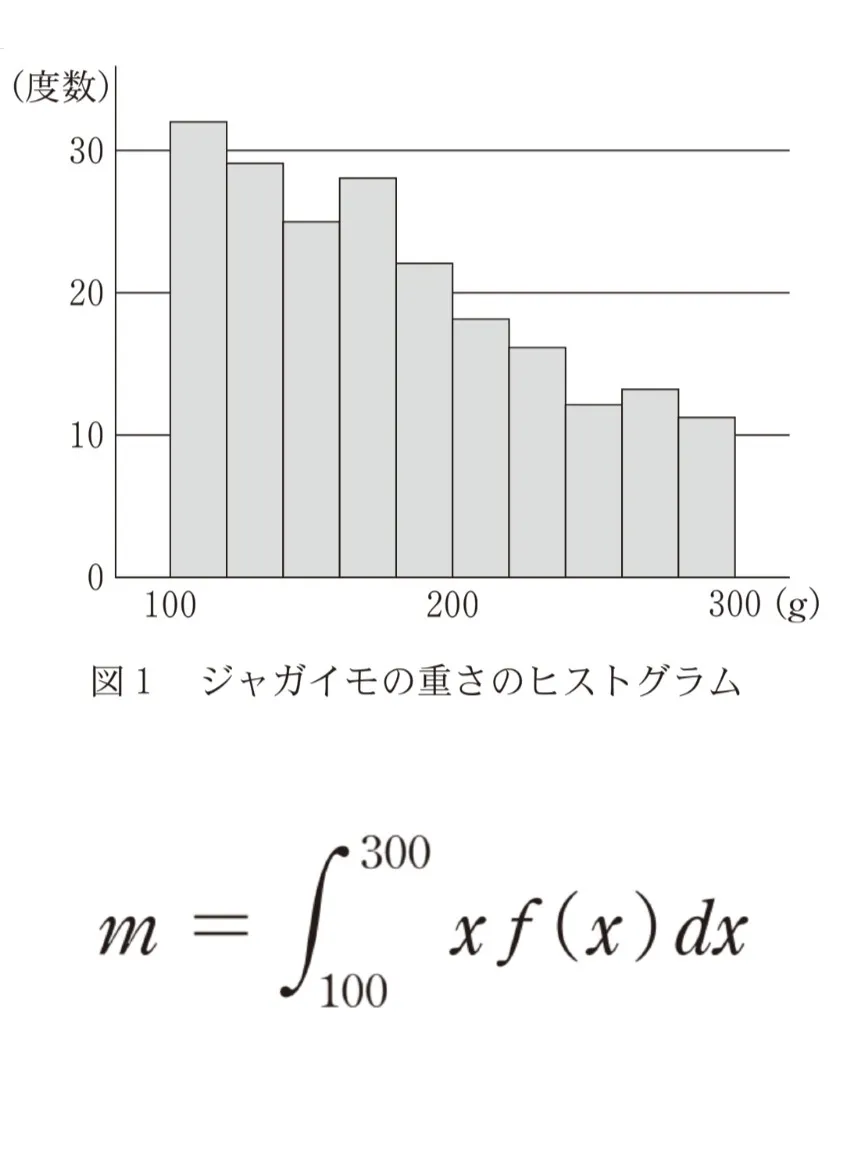
B地区で収穫され、出荷される予定のジャガイモから206個を無作為に抽出したところ、重さの標本平均は180gであった。図1はこの標本のヒストグラムである。
花子さんは図1のヒストグラムにおいて、重さxの増加とともに度数がほぼ一定の割合で減少している傾向に着目し、Xの確率密度関数f(x)として、1次関数
f(x)=ax+b(100≦x≦300)
を考えることにした。ただし、100≦x≦300の範囲でf(x)≧0とする。
このとき、P(100≦X≦300)=( ク )であることから
( ケ )・104a+( コ )・102b=( ク )・・・・・①
である。
花子さんは、Xの平均(期待値)が重さの標本平均180gと等しくなるように確率密度関数を定める方法を用いることにした。
連続型確率変数Xのとり得る値xの範囲が100≦x≦300で、その確率密度関数がf(x)のとき、Xの平均(期待値)mは
画像内の式で定義される。
m=26/3・106a+4・104b=180・・・・・②
となる。①と②により、確率密度関数は
f(x)=( −サ )・10−5x+( シス )・10−3・・・・・③
と得られる。このようにして得られた③のf(x)は、100≦x≦300の範囲でf(x)≧0を満たしており、確かに確率密度関数として適当である。
したがって、この花子さんの方針に基づくと、B地区で収穫され、出荷される予定のすべてのジャガイモのうち、重さが200g以上のものは( セ )%あると見積もることができる。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)本試験 問92(数学Ⅱ・数学B(第3問) 問8) (訂正依頼・報告はこちら)
問題を解答するにあたっては、必要に応じて 正規分布表(リンク) を用いてもよい。
ジャガイモを栽培し販売している会社に勤務する花子さんは、A地区とB地区で収穫されるジャガイモについて調べることになった。
(3)B地区で収穫され、出荷される予定のジャガイモ1個の重さは100gから300gの間に分布している。B地区で収穫され、出荷される予定のジャガイモ1個の重さを表す確率変数をXとするとき、Xは連続型確率変数であり、Xのとり得る値xの範囲は100≦x≦300である。
花子さんは、B地区で収穫され、出荷される予定のすべてのジャガイモのうち、重さが200g以上のものの割合を見積もりたいと考えた。そのために花子さんは、Xの確率密度関数f(x)として適当な関数を定め、それを用いて割合を見積もるという方針を立てた。
B地区で収穫され、出荷される予定のジャガイモから206個を無作為に抽出したところ、重さの標本平均は180gであった。図1はこの標本のヒストグラムである。
花子さんは図1のヒストグラムにおいて、重さxの増加とともに度数がほぼ一定の割合で減少している傾向に着目し、Xの確率密度関数f(x)として、1次関数
f(x)=ax+b(100≦x≦300)
を考えることにした。ただし、100≦x≦300の範囲でf(x)≧0とする。
このとき、P(100≦X≦300)=( ク )であることから
( ケ )・104a+( コ )・102b=( ク )・・・・・①
である。
花子さんは、Xの平均(期待値)が重さの標本平均180gと等しくなるように確率密度関数を定める方法を用いることにした。
連続型確率変数Xのとり得る値xの範囲が100≦x≦300で、その確率密度関数がf(x)のとき、Xの平均(期待値)mは
画像内の式で定義される。
m=26/3・106a+4・104b=180・・・・・②
となる。①と②により、確率密度関数は
f(x)=( −サ )・10−5x+( シス )・10−3・・・・・③
と得られる。このようにして得られた③のf(x)は、100≦x≦300の範囲でf(x)≧0を満たしており、確かに確率密度関数として適当である。
したがって、この花子さんの方針に基づくと、B地区で収穫され、出荷される予定のすべてのジャガイモのうち、重さが200g以上のものは( セ )%あると見積もることができる。

- 10
- 11
- 12
- 13
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
解答 シス: 11
解説
サシスを合わせて解説します(以下、直前のサと同じ解説文です)。
前問より ク:1 ケ: 4 コ: 2 でした。つまり
4・104a + 2・102b = 1 …①
です。また、問題文より
(26/3)・106a + 4・104b = 180 …②
です。この2式①②をaとbの連立方程式と見て解きます。
解きやすいように変形しましょう。あくまで一例ですが、
①×300 より 12・106a + 6・104b = 300 …①’
②×(3/2)より 13・106a + 6・104b = 270 …②’
として①’ - ②’ より -106a = 30 よって a = -3・10-5 ←サの答え
①に代入して -1.2 + 2・ 102b = 1 よって b = 11・10-3 ←シスの答え
のように解くとよいでしょう。
まとめると、a = -3・10-5 b = 11・10-3 であり、
確率密度関数は f(x) = -3・10-5 x + 11・10-3 …③ と求まります。
よって答えは a = -3・10-5 b = 11・10-3
つまり サ: 3 シス: 11 となります。
補足
以下はクケコの解説です(前問より引用)。
クの解説
ケコの解説
この選択肢が正解となります。
参考になった数0
この解説の修正を提案する
前の問題(問91)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問93)へ