大学入学共通テスト(数学) 過去問
令和6年度(2024年度)追・試験
問98 (数学Ⅱ・数学B(第4問) 問8)
問題文
y=2x ・・・・・①
y=mx+4 ・・・・・②
を考える。
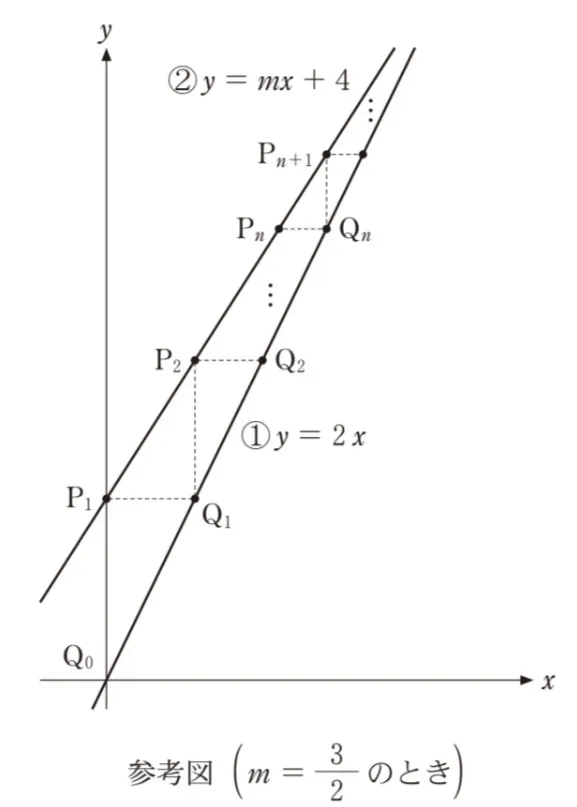
原点(0,0)をQ0、点(0,4)をP1とし、次の手順で点Q1、P2、Q2、…、Pn、Qn、Pn+1、…を定める。
<手順>
・P1からx軸に平行な直線を引いて、直線①との交点をQ1とする。
・Q1からy軸に平行な直線を引いて、直線②との交点をP2とする。
・・・
・Pnからx軸に平行な直線を引いて、直線①との交点をQnとする。
・Qnからy軸に平行な直線を引いて、直線②との交点をPn+1とする。
・・・
(2)m=−1とする。すなわち、②はy=−x+4である。自然数nについて、
Pnのy座標をbnとする。
(ⅰ)数列{bn}について、b1=( ク )かつ
bn+1=([ ケコ ]/[ サ ])bn+( シ ) (n=1、2、3、…)
となる。よって、数列{bn}の一般項は
bn=([ ス ]/[ セ ])([ ソタ ]/[ チ ])>n−1+([ ツ ]/[ テ ])
となる。
(ⅱ)自然数nについて、Qn−1とPnを結ぶ線分の長さをcnとし、PnとQnを結ぶ線分の長さをdnとする。Q0、P1、Q1、P2、…、Pn、Qnを順に結んだ折れ線の長さをSnとおく。Sn=c1+d1+c2+d2+…+cn+dnである。
すべての自然数nについて、dnをcnを用いて表すと、dn=( ト )である。また、数列{cn}について
cn+1=( ナ ) (n=1、2、3、…)
が成り立つ。このことを用いると
Sn=( ニ ) (n=1、2、3、…)
となる。
( ト )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)追・試験 問98(数学Ⅱ・数学B(第4問) 問8) (訂正依頼・報告はこちら)
y=2x ・・・・・①
y=mx+4 ・・・・・②
を考える。
原点(0,0)をQ0、点(0,4)をP1とし、次の手順で点Q1、P2、Q2、…、Pn、Qn、Pn+1、…を定める。
<手順>
・P1からx軸に平行な直線を引いて、直線①との交点をQ1とする。
・Q1からy軸に平行な直線を引いて、直線②との交点をP2とする。
・・・
・Pnからx軸に平行な直線を引いて、直線①との交点をQnとする。
・Qnからy軸に平行な直線を引いて、直線②との交点をPn+1とする。
・・・
(2)m=−1とする。すなわち、②はy=−x+4である。自然数nについて、
Pnのy座標をbnとする。
(ⅰ)数列{bn}について、b1=( ク )かつ
bn+1=([ ケコ ]/[ サ ])bn+( シ ) (n=1、2、3、…)
となる。よって、数列{bn}の一般項は
bn=([ ス ]/[ セ ])([ ソタ ]/[ チ ])>n−1+([ ツ ]/[ テ ])
となる。
(ⅱ)自然数nについて、Qn−1とPnを結ぶ線分の長さをcnとし、PnとQnを結ぶ線分の長さをdnとする。Q0、P1、Q1、P2、…、Pn、Qnを順に結んだ折れ線の長さをSnとおく。Sn=c1+d1+c2+d2+…+cn+dnである。
すべての自然数nについて、dnをcnを用いて表すと、dn=( ト )である。また、数列{cn}について
cn+1=( ナ ) (n=1、2、3、…)
が成り立つ。このことを用いると
Sn=( ニ ) (n=1、2、3、…)
となる。
( ト )にあてはまるものを1つ選べ。

- (1/2)cn
- cn
- 2cn
- cn−2
- −(1/2)cn+4
- −cn+2
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
便宜上、点Qn(Qnx,Qny)と表現いたします。
題意よりP1y=b1=4
各点をプロットしていくと
Pn( ,bn)
Pny=Qnyとy=2xより
Qn(bn/2,bn)
Pn+1x=Qnxとy=-x+4より
Pn+1(bn/2,-bn/2+4)
従ってbn+1=-bn/2+4
bnの漸化式は等比も等差も相まっている場合であるため置換する必要があります。
ここでbn+1=bn=bとすると
b=-b/2+4
↔b=8/3
従って漸化式は
bn+1-8/3=-1/2(bn-8/3)
と変形できる。ここでBn=bn-8/3と置換すると
Bn+1=-Bn/2
また
B1=b1-8/3=4-8/3=4/3
従ってBn=4/3(-1/2)n-1と書くことができます。
従って
bn-8/3=4/3(-1/2)n-1
↔bn=4/3(-1/2)n-1+8/3
ここで各点を図示すると下図のようになります。
ここで青い三角形や赤い三角形は相似であるから
cn:dn=4:2
↔2cn=4dn
↔dn=cn/2
正解です。
不正解です。
不正解です。
不正解です。
不正解です。
不正解です。
相似の関係性であることに気づけるかがpointです。
参考になった数0
この解説の修正を提案する
前の問題(問97)へ
令和6年度(2024年度)追・試験 問題一覧
次の問題(問99)へ