大学入学共通テスト(数学) 過去問
令和7年度(2025年度)本試験
問62 (数学Ⅱ・数学B(第2問) 問6)
問題文
学校の池でメダカを飼うことが決まり、メダカの飼育係になった花子さんは、水質を良くする効果がある水草Aを水面に浮かべることにした。一方で、水草Aが増えすぎてメダカに悪影響を与えることを心配した花子さんは、水草Aを定期的に除去することにし、その作業の計画を立てるために次の基本方針を定めた。
基本方針
・水草Aの量を水草Aが池の水面を覆う面積の割合(%)で測ることにし、この量をもとに作業計画を立てる。
・作業は正午に行う。
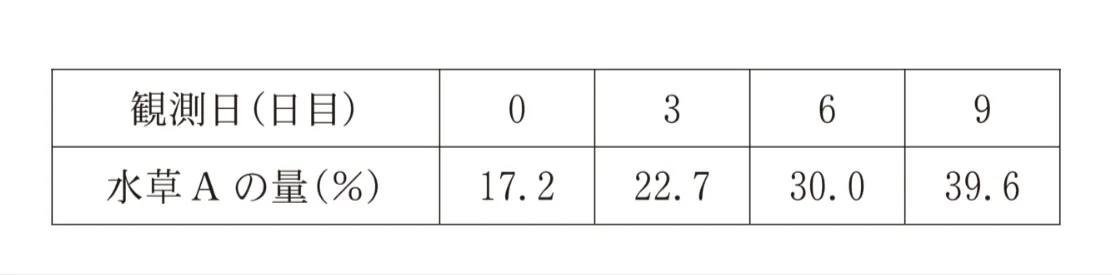
(1)水草Aの増え方を知るために、観測を行った。後の表は、観測を開始した日を0日目として、0日目、3日目、6日目、9日目の正午に観測した水草Aの量を表したものである。
水草Aの量が3日ごとに何倍に増えるのかを計算して小数第3位を四捨五入したところ、いずれも1.32倍であることがわかった。水草Aの量は、3日ごとにほとんど同じ倍率で増えていることから、「水草Aの量は、1日ごとに一定の倍率で増える」と考え、その倍率を定数rとした。
観測結果から、3日目の水草Aの量は0日目の量の1.32倍になると考えた。
このとき、rは( ア )=1.32を満たす。
log101.32=( イ )であるので
log10r=0.( ウエオカ )
が得られる。
(2)花子さんは、基本方針に次の条件を加えて、作業計画を立てることにした。
条件
・作業は14日ごとに行う。
・作業の後に残す水草Aの量を、次回の作業までの間に水草Aの量がつねに60%を超えない範囲で、できるだけ多くする。
作業の後に残す水草Aの量について考える。
作業を行った日を0日目として、次回の作業は14日目に行う。なお、作業にかかる時間は考えないものとする。
次のような実数aを考える。作業の後に残す水草Aの量をa%としたとき、14日目の正午に水草Aの量がちょうど60%になる。
このとき、(1)の定数rを用いると、14日目の正午に水草Aの量はaの( キ )倍になるので
a✕( キ )=( クケ )・・・・・①
が成り立つ。
①の両辺の常用対数をとり、(1)で求めたlog10r=0.( ウエオカ )とlog106=0.7782であることを用いると、log10a=( コ )となる。
aの決め方から、作業の後に残す水草Aの量をa%以下にすれば、次回の作業までの間に水草Aの量がつねに60%を超えないことがわかる。a以下で最大の整数は( サシ )であることから、花子さんは作業の後に残す水草Aの量を( サシ )%にすることとした。
( コ )について、最も適当なものを、次のうちから一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和7年度(2025年度)本試験 問62(数学Ⅱ・数学B(第2問) 問6) (訂正依頼・報告はこちら)
学校の池でメダカを飼うことが決まり、メダカの飼育係になった花子さんは、水質を良くする効果がある水草Aを水面に浮かべることにした。一方で、水草Aが増えすぎてメダカに悪影響を与えることを心配した花子さんは、水草Aを定期的に除去することにし、その作業の計画を立てるために次の基本方針を定めた。
基本方針
・水草Aの量を水草Aが池の水面を覆う面積の割合(%)で測ることにし、この量をもとに作業計画を立てる。
・作業は正午に行う。
(1)水草Aの増え方を知るために、観測を行った。後の表は、観測を開始した日を0日目として、0日目、3日目、6日目、9日目の正午に観測した水草Aの量を表したものである。
水草Aの量が3日ごとに何倍に増えるのかを計算して小数第3位を四捨五入したところ、いずれも1.32倍であることがわかった。水草Aの量は、3日ごとにほとんど同じ倍率で増えていることから、「水草Aの量は、1日ごとに一定の倍率で増える」と考え、その倍率を定数rとした。
観測結果から、3日目の水草Aの量は0日目の量の1.32倍になると考えた。
このとき、rは( ア )=1.32を満たす。
log101.32=( イ )であるので
log10r=0.( ウエオカ )
が得られる。
(2)花子さんは、基本方針に次の条件を加えて、作業計画を立てることにした。
条件
・作業は14日ごとに行う。
・作業の後に残す水草Aの量を、次回の作業までの間に水草Aの量がつねに60%を超えない範囲で、できるだけ多くする。
作業の後に残す水草Aの量について考える。
作業を行った日を0日目として、次回の作業は14日目に行う。なお、作業にかかる時間は考えないものとする。
次のような実数aを考える。作業の後に残す水草Aの量をa%としたとき、14日目の正午に水草Aの量がちょうど60%になる。
このとき、(1)の定数rを用いると、14日目の正午に水草Aの量はaの( キ )倍になるので
a✕( キ )=( クケ )・・・・・①
が成り立つ。
①の両辺の常用対数をとり、(1)で求めたlog10r=0.( ウエオカ )とlog106=0.7782であることを用いると、log10a=( コ )となる。
aの決め方から、作業の後に残す水草Aの量をa%以下にすれば、次回の作業までの間に水草Aの量がつねに60%を超えないことがわかる。a以下で最大の整数は( サシ )であることから、花子さんは作業の後に残す水草Aの量を( サシ )%にすることとした。
( コ )について、最も適当なものを、次のうちから一つ選べ。

- 0.7758
- 1.0670
- 1.0934
- 1.2154
- 1.3410
- 1.4894
- 1.7806
- 2.4666
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問61)へ
令和7年度(2025年度)本試験 問題一覧
次の問題(問63)へ