大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問109 (数学Ⅱ・数学B(第5問) 問5)
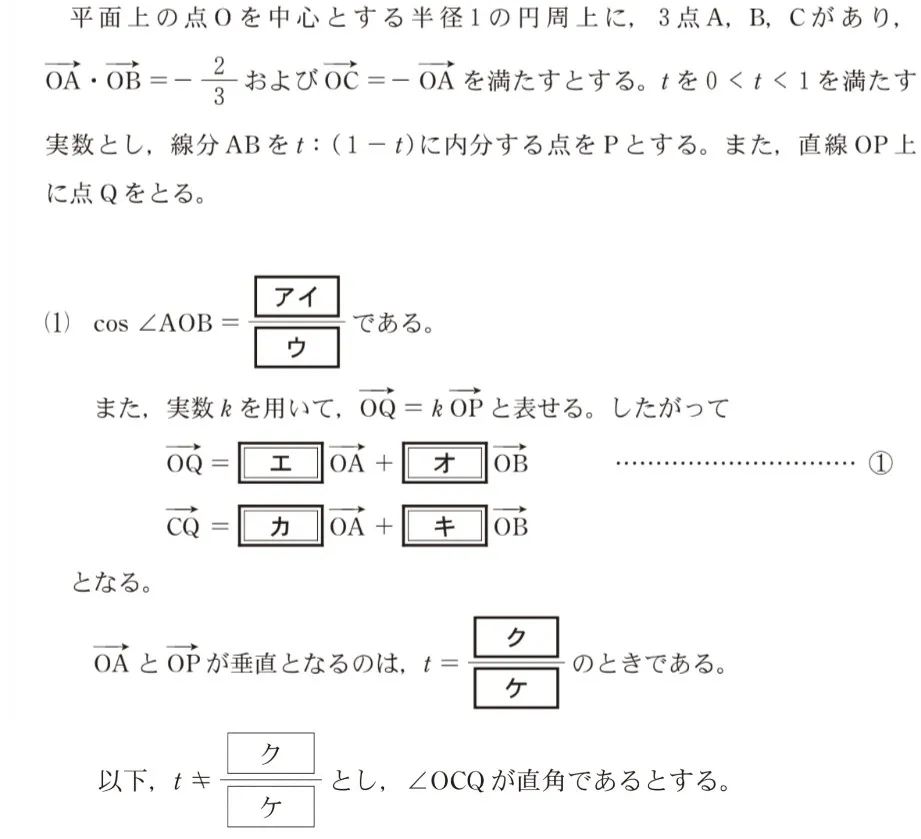
問題文
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)本試験 問109(数学Ⅱ・数学B(第5問) 問5) (訂正依頼・報告はこちら)

- kt
- (k−kt)
- (kt+1)
- (kt−1)
- (k−kt+1)
- (k−kt−1)
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
解答 キ: kt
解説
【表記に関する注意】
ここではベクトルを上に矢印をつけず右に添えて「OA→」などのように表記します。
カとキを合わせて解説します。
以下は直前の問題(カ)と全く同一の解説文になります。
前問より エ: (k-kt) オ: kt つまり
(OQ→) = (k-kt) (OA→) + kt (OB→) …①
でした。
問題文より、
(OC→) = - (OA→) つまり (CO→) = (OA→)
であることに注意して、
(CQ→)
= (CO→) + (OQ→)
= (OA→) + (k-kt) (OA→) + kt (OB→) (①を代入)
= (k-kt+1) (OA→) + kt (OB→)
よって答えは カ: (k-kt+1) キ: kt となります。
補足
以下はエとオの解説です(前問より引用)。
この選択肢が答えとなります。
参考になった数0
この解説の修正を提案する
02
※この問題では「ベクトルa」を「→a」と表記します。
(カ)と同様です。
→CQを→OAと→OBで表す問題です。
いきなり→OAと→OBで表すのは難しそうなので、まずは→CQを言い換えます。
ベクトルの引き算の定義より、
→CQ=(→OQ)−(→OC)・・・・・(*)
→OQと→OCをそれぞれ→OAと→OBを用いて表し、(*)に代入しましょう。
(エ)・(オ)より、
→OQ=(k-kt)(→OA)+kt(→OB)
また問題文より、
→OC=−(→OA)
これらを(*)に代入すると、
→CQ={(k-kt)(→OA)+kt(→OB)}−(−(→OA))
となります。これを展開することによって、
→CQ=(k-kt+1)→OA + kt(→OB)
と表せます。
→CQ=(k-kt+1)→OA + kt(→OB)
より正解
→CQ=(k-kt+1)→OA + kt(→OB)
より誤り
→CQ=(k-kt+1)→OA + kt(→OB)
より誤り
→CQ=(k-kt+1)→OA + kt(→OB)
より誤り
→CQ=(k-kt+1)→OA + kt(→OB)
より誤り
→CQ=(k-kt+1)→OA + kt(→OB)
より誤り
→CQなどのよくわからないベクトルが出てきたら、正体のわかっているベクトルで言い換えて見通しをよくすることができます。
ベクトルの引き算の計算をスムーズにできるようにしておきましょう。
参考になった数0
この解説の修正を提案する
前の問題(問108)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問110)へ