大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問117 (数学Ⅱ・数学B(第5問) 問13)
問題文
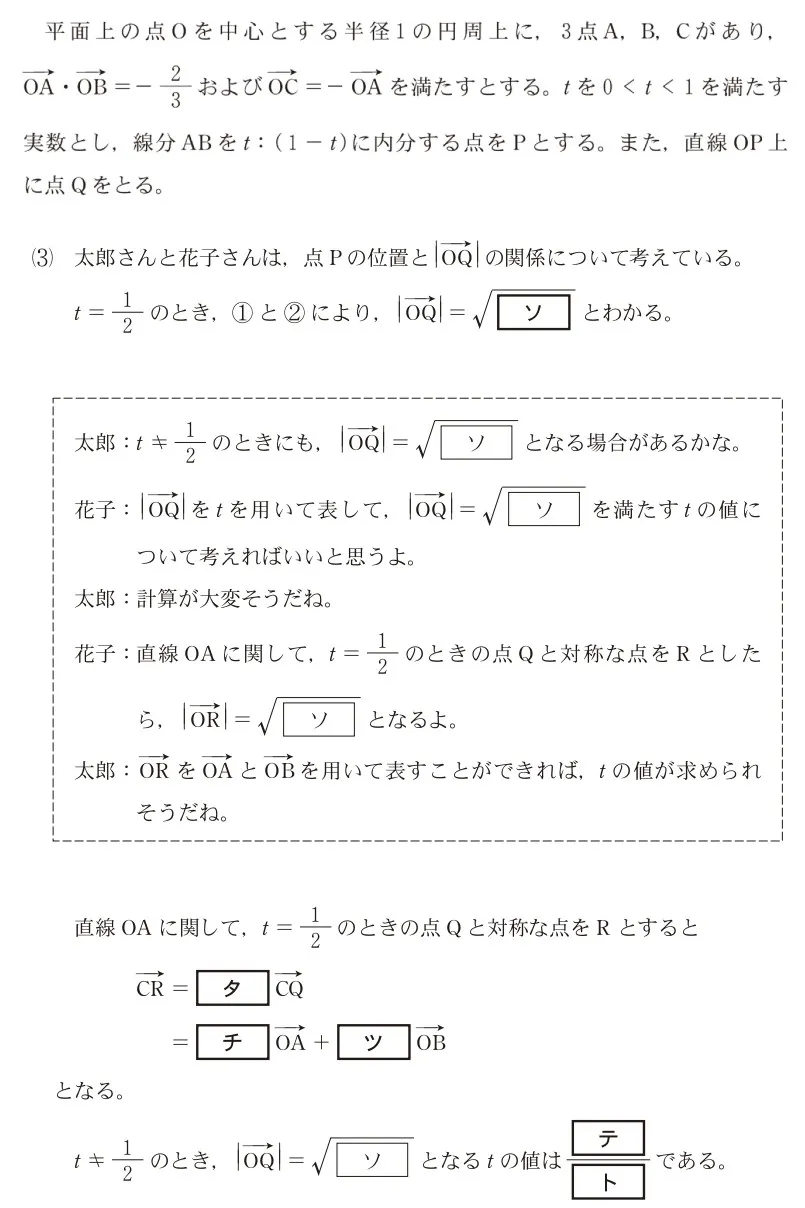
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)本試験 問117(数学Ⅱ・数学B(第5問) 問13) (訂正依頼・報告はこちら)

- 1/3
- 2/4
- 3/5
- 3/4
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
解答 テ: 3 ト: 4 (3/4)
解説
【表記に関する注意】
ここではベクトルを上に矢印をつけず右に添えて「OA→」などのように表記します。
この問題ではエ・オ・チ・ツの答えを利用します。
t≠1/2 のときに|OQ→| = √6 となるようなtの値を求めます。
問題文の誘導に従い、|OR→| = √6 となるようなtの値を求めましょう。
まず(OR→)を(OA→)と(OB→)を用いて表した式を求めます。
前問より チ: 2 ツ: 3 つまり
(CR→)=2 (OA→) + 3 (OB→)
でした。これを用いて、
(OR→)
= (OC→)+(CR→)
= -(OA→)+2(OA→)+3(OB→) (問題文中の(OC→) = -(OA→)より)
= (OA→)+3(OB→) …(式1)
となります。
一方、①(エ: k-kt オ: kt)と同様に考えて
(OR→) = (k-kt) (OA→) + kt (OB→) …(式2)
となります。
(式1)と(式2)の(OA→)と(OB→)の係数を比較して、
「k-kt = 1 かつ kt = 3」
となります。これをkとtの連立方程式と見て解きます。
2式を足して k=4 となります。
これを kt = 3に代入して 4t=3 つまり t=3/4 です。
よって答えは t = 3/4 つまり テ: 3 ト: 4 となります。
あるいは(式1)について、
(OA→) の係数「1」と(OB→)の係数「3」の和である「4」で式全体をくくると、
(OR→) = (OA→) + 3 (OB→) = 4{(1/4)(OA→) + (3/4)(OB→)}
であり、ここから
「Oを始点、線分ABを(1/4):(3/4)に内分する点を終点したベクトルの4倍が(OR→)である」
と読み取ることができれば、直ちに t = 3/4 (テ: 3 ト: 4) が得られます。
補足
以下はエ・オ・チ・ツの解説です(前問より引用)。
エ・オの解説
チ・ツの解説
この選択肢が答えとなります。
参考になった数0
この解説の修正を提案する
02
※この問題では「ベクトルa」を「→a」と表記します。
(チ)・(ツ)より
→CR=2(→OA)+3(→OB)
なので、
→OR=(→CR)−(→CO)=(→CR)−(→OA)=2(→OA)+3(→OB)−(→OA)=→OA+3(→OB)
つまり、
→OR=→OA+3(→OB)
です。
ここで上の図(t=1/2)と下の図(t≠1/2)のように、tの値によって同じ位置でもRとQの位置が入れ替わるtがあります(Pの位置は変化していますね)。
よって、「t=1/2のときの→OR」が「t≠1/2のときの→OQ」と等しくなるt(≠1/2)があるはずです。
ここで
→OQ=(k-kt)(→OA)+kt(→OB)
と表すことができたので、
→OA+3(→OB)=(k-kt)(→OA)+kt(→OB)
となるk,tの値を求めれば良いです。
→OA、→OBの係数をそれぞれ比較することによって(→OAと→OBは1次独立より可能)、
k-kt=1
kt=3
の連立方程式を解いて、
k=4
t=3/4
と求められます。
t=3/4より誤りです。
t=3/4より誤りです。
t=3/4より誤りです。
t=3/4より正解です。
「tの値によって、RとQの位置が入れ替わる瞬間が存在する」ということが見抜けないと難しい問題でした。
もちろん別解もあり、→OQを全てtの式で表して(kを消去)、|→OQ|=√6というなるtを求めても良いでしょうが、かなり時間がかかります。
参考になった数0
この解説の修正を提案する
前の問題(問116)へ
令和4年度(2022年度)本試験 問題一覧