大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問116 (数学Ⅱ・数学B(第5問) 問12)
問題文
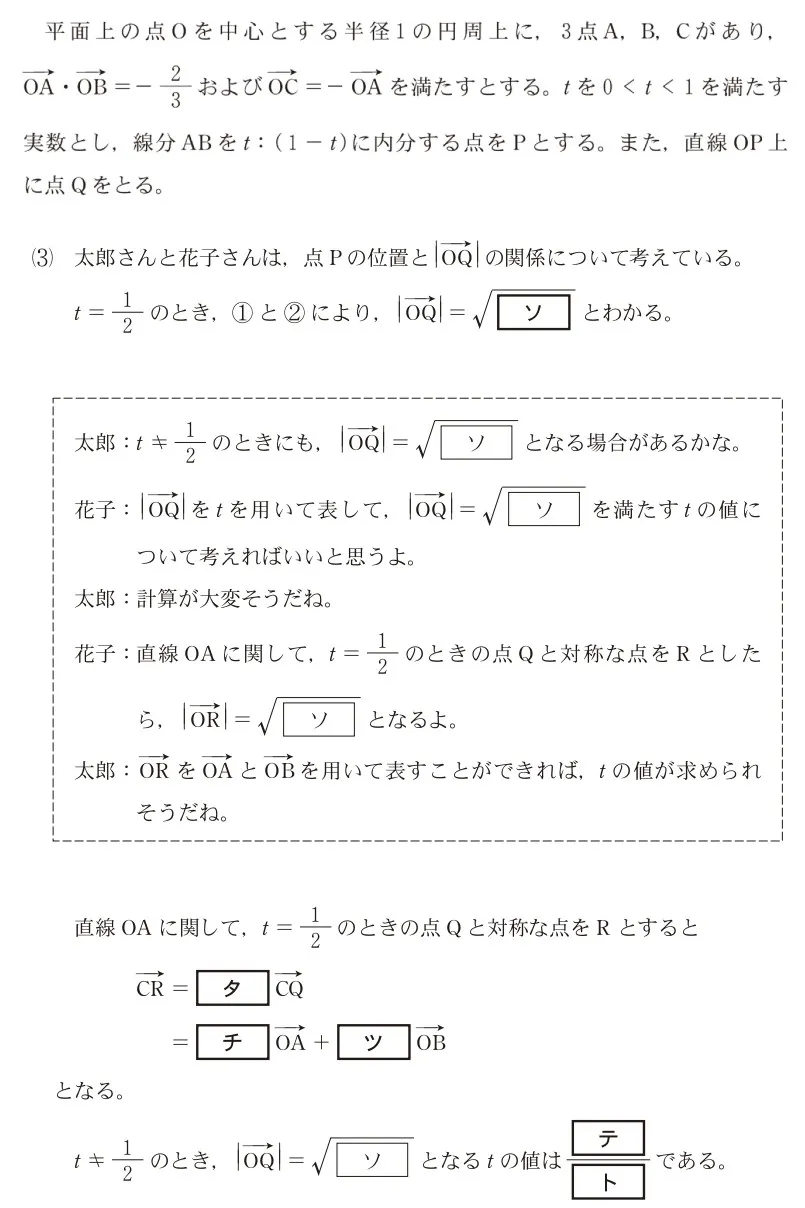
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)本試験 問116(数学Ⅱ・数学B(第5問) 問12) (訂正依頼・報告はこちら)

- チ:2 ツ:3
- チ:3 ツ:4
- チ:2 ツ:5
- チ:2 ツ:4
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
解答 チ: 2 ツ: 3
解説
【表記に関する注意】
ここではベクトルを上に矢印をつけず右に添えて「OA→」などのように表記します。
ソの答えを求める過程で、t = 1/2のときに
(OQ→) = -3 (OA→) -3 (OB→) …①’’
であることを求めました(この解説はここでは省略)。これを利用します。
まず、直線OAに関して点Qと対称な点をRとして、前問で考えた通り
(CR→) = -(CQ→)
です(簡潔な解説: RQとOAは点Cで直交し、点CはRQの中点になっている)。
(CR→)
= -(CQ→)
= (QC→)
= (OC→) - (OQ→) (始点をOにそろえる)
= -(OA→) + 3(OA→)+3 (OB→) (①’’と問題文中の(OC→)=-(OA→)より)
= 2(OA→)+3 (OB→)
よって答えは (CR→)=2 (OA→) + 3 (OB→) つまり チ: 2 ツ: 3 となります。
この選択肢が答えとなります。
参考になった数0
この解説の修正を提案する
02
※この問題では「ベクトルa」を「→a」と表記します。
(タ)より
→CR=−(→CQ)
でした。
また、(カ)・(キ)より、
→CQ=(k-kt+1)→OA + kt(→OB)・・・・・(*)
でした。
いま、t=1/2なので、②よりk=−6となっています。
よってこれらを(*)に代入して、
→CQ=(−6−(−6)×(1/2)+1)(→OA)+(−6)×(1/2)(→OB)=−2(→OA)−3(→OB)
となります。
→CR=−(→CQ)より、
→CR=2(→OA)+3(→OB)
となります。
→CR=2(→OA)+3(→OB)より正しいです。
→CR=2(→OA)+3(→OB)より誤りです。
→CR=2(→OA)+3(→OB)より誤りです。
→CR=2(→OA)+3(→OB)より誤りです。
今までに解いた問題の蓄積を総動員する問題でした。共通テストの終盤ではこのような出題がされることが多いので、前の結果にも気を配りつつ解いていきましょう。
参考になった数0
この解説の修正を提案する
前の問題(問115)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問117)へ