大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問115 (数学Ⅱ・数学B(第5問) 問11)
問題文
空欄( タ )に当てはまるものを選べ。 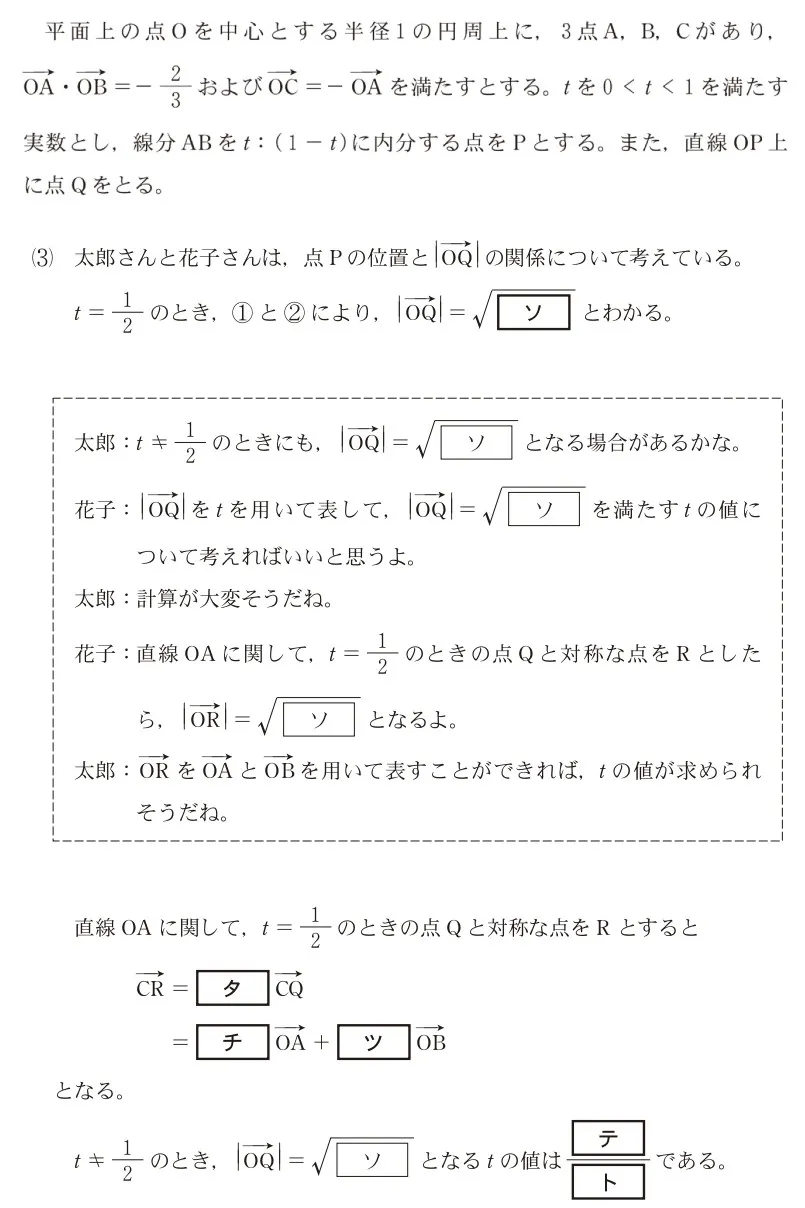

このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
正解!素晴らしいです
残念...
MENU
あ
か
さ
た
な
は
ま
や
ら
あん摩マッサージ指圧師
1級管工事施工管理技士
1級建築施工管理技士
1級電気工事施工管理技士
1級土木施工管理技士
運行管理者(貨物)
2級ファイナンシャル・プランニング技能士(FP2級)
3級ファイナンシャル・プランニング技能士(FP3級)
貸金業務取扱主任者
危険物取扱者(乙4)
給水装置工事主任技術者
クレーン・デリック運転士
ケアマネジャー(介護支援専門員)
国内旅行業務取扱管理者
社会保険労務士(社労士)
大学入学共通テスト(国語)
大学入学共通テスト(地理歴史)
大学入学共通テスト(公民)
大学入学共通テスト(数学)
大学入学共通テスト(理科)
大学入学共通テスト(情報)
大学入学共通テスト(英語)
第三種電気主任技術者(電験三種)
宅地建物取引士(宅建士)
調剤報酬請求事務技能認定
賃貸不動産経営管理士
2級管工事施工管理技士
2級建築施工管理技士
2級電気工事施工管理技士
2級土木施工管理技士
JLPT(日本語能力)
建築物環境衛生管理技術者(ビル管理士)
問題文

このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
正解!素晴らしいです
残念...
この過去問の解説 (2件)
01
解答 タ: - (マイナス)
解説
【表記に関する注意】
ここではベクトルを上に矢印をつけず右に添えて「OA→」などのように表記します。
図を描くとすぐにわかりますが、言葉で説明しておきます。
点Rは直線OAに関して点Qと対称な点ですから、
直線OA上に点Cがあることに注意して、
「∠OCR = ∠OCQ かつ CR=CQ」
となります。∠OCQが直角であるため、∠OCRも直角となり、
3点R、C、Qはこの順に一直線上に並びます。
これとCR = CQを踏まえると、 (CR→) = -(CQ→) が成り立ちます。
よって答えは タ: - (マイナス) です。
なお、この設問ではt=1/2の条件は使いません。
この選択肢が答えとなります。
参考になった数0
この解説の修正を提案する
02
※この問題では「ベクトルa」を「→a」と表記します。
点Rは点QをACを軸に対象に移動させた点です。
よって、CRとCQの長さは等しいです。
ここで、→CRと→CQは逆向きなので、
→CR=−(→CQ)
となります。
→CR=−(→CQ)より誤りです。
→CR=−(→CQ)より正しいです。
図を書くと、ベクトルの向きが逆であることがわかります。
参考になった数0
この解説の修正を提案する
前の問題(問114)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問116)へ