大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問114 (数学Ⅱ・数学B(第5問) 問10)
問題文
空欄( ソ )に当てはまるものを選べ。 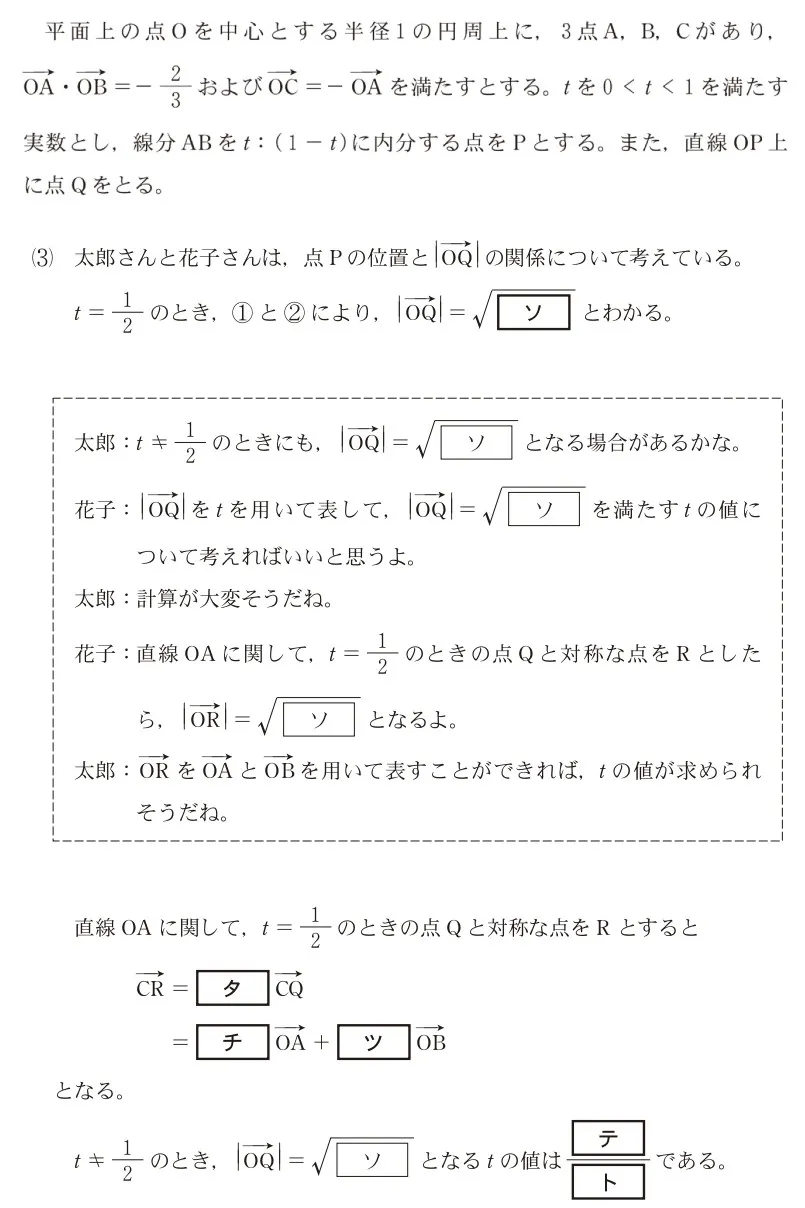

このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
正解!素晴らしいです
残念...
MENU
あ
か
さ
た
な
は
ま
や
ら
あん摩マッサージ指圧師
1級管工事施工管理技士
1級建築施工管理技士
1級電気工事施工管理技士
1級土木施工管理技士
運行管理者(貨物)
2級ファイナンシャル・プランニング技能士(FP2級)
3級ファイナンシャル・プランニング技能士(FP3級)
貸金業務取扱主任者
危険物取扱者(乙4)
給水装置工事主任技術者
クレーン・デリック運転士
ケアマネジャー(介護支援専門員)
国内旅行業務取扱管理者
社会保険労務士(社労士)
大学入学共通テスト(国語)
大学入学共通テスト(地理歴史)
大学入学共通テスト(公民)
大学入学共通テスト(数学)
大学入学共通テスト(理科)
大学入学共通テスト(情報)
大学入学共通テスト(英語)
第三種電気主任技術者(電験三種)
宅地建物取引士(宅建士)
調剤報酬請求事務技能認定
賃貸不動産経営管理士
2級管工事施工管理技士
2級建築施工管理技士
2級電気工事施工管理技士
2級土木施工管理技士
JLPT(日本語能力)
建築物環境衛生管理技術者(ビル管理士)
問題文

このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
正解!素晴らしいです
残念...
この過去問の解説 (2件)
01
解答 ソ: 6
解説
【表記に関する注意】
ここではベクトルを上に矢印をつけず右に添えて「OA→」などのように表記します。
①②を用いて、t=1/2のときの|OQ→|を求める問題です。
|OQ→|2を求め、その正の平方根を考えます。
まずt=1/2のときの(OQ→)を求めます。
前問より
エ: (k-kt) オ: kt コ: 3 サ: 5 シ: 3
つまり
(OQ→) = (k-kt) (OA→) + kt (OB→) …①
k = 3/(5t-3) …②
です。①②に t = 1/2 を代入して、
(OQ→) = (1/2)k (OA→) + (1/2)k (OB→) …①’
k = 3/((5/2)-3) = 6/(5-6) = -6 …②’
であり、②’を①’に代入して
(OQ→) = -3 (OA→) -3 (OB→) = -3 {(OA→)+(OB→)} …①’’
となります。
|OA→|=|OB→|=1 、(OA→)・(OB→) = -2/3
であることに注意して、①’’を用いて|OQ→|2を計算します。
|OQ→|2
= (OQ→)・(OQ→)
= 9 ((OA→)+(OB→))・((OA→)+(OB→))
= 9 (|OA→|2 + 2(OA→)・(OB→) + |OB→|2)
= 9 (1 - 4/3 + 1)
= 9・2/3
= 6
よって答えは |OQ→| = √6 つまり ソ: 6 となります。
補足
以下は①②を求めるのに必要なエ~シの解説です(前問より引用)。
エ・オの解説
カ・キの解説
ク・ケの解説
ここでは大幅に解説を省略します。
「(OA→)・(OP→) = 0」⇔「t = 3/5」 より ク: 3 ケ: 5 です。
次のコサシは t ≠ 3/5 のもとで考えます。
コ・サ・シの解説
この選択肢が答えとなります。
ベクトル(a→)の大きさ|a→|を求めるために
いったん2乗して |a→|2=(a→)・(a→) を用いる場合がよくあります。
この「2乗する」という解法はポイントとして押さえておきましょう。
参考になった数0
この解説の修正を提案する
02
※この問題では「ベクトルa」を「→a」と表記します。
(2)より、k=3/(5t-3)
(1)より、→OQ=(k-kt)(→OA)+kt(→OB)
でした。
これらにt=1/2を代入すると、
k=-6
→OQ={−6−(−6)(1/2)}(→OA)+(−6)(1/2)(→OB)=−3(→OA)−3(→OB)
となります。
|→OQ|、つまり→OQの大きさを求めたいです。ベクトルの大きさを求めるときは二乗をするのが定石です。
|→OQ|2=( −3(→OA)−3(→OB) )2=9|→OA|2−18(→OA・→OB)+9|→OB|2
ここに、
|→OA|=|→OB|=1 (∵OA, OBは円の半径)
→OA・→OB=-2/3 (問題文より)
を代入すると、
|→OQ|2=9・12−18(−2/3)+9・12=6
したがって、
|→OQ|=√6
となります。
|→OQ|=√6なので誤りです。
|→OQ|=√6なので正解です。
|→OQ|=√6なので誤りです。
|→OQ|=√6なので誤りです。
ベクトルの大きさを求めたい⇒二乗を計算
その際に出てくるベクトルの大きさ(|→a|2など)や、ベクトルの内積(→a・→b など)を代入することによって、求めることができます。
最後に√をつけるのを忘れないようにしましょう。
参考になった数0
この解説の修正を提案する
前の問題(問113)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問115)へ