大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問113 (数学Ⅱ・数学B(第5問) 問9)
問題文
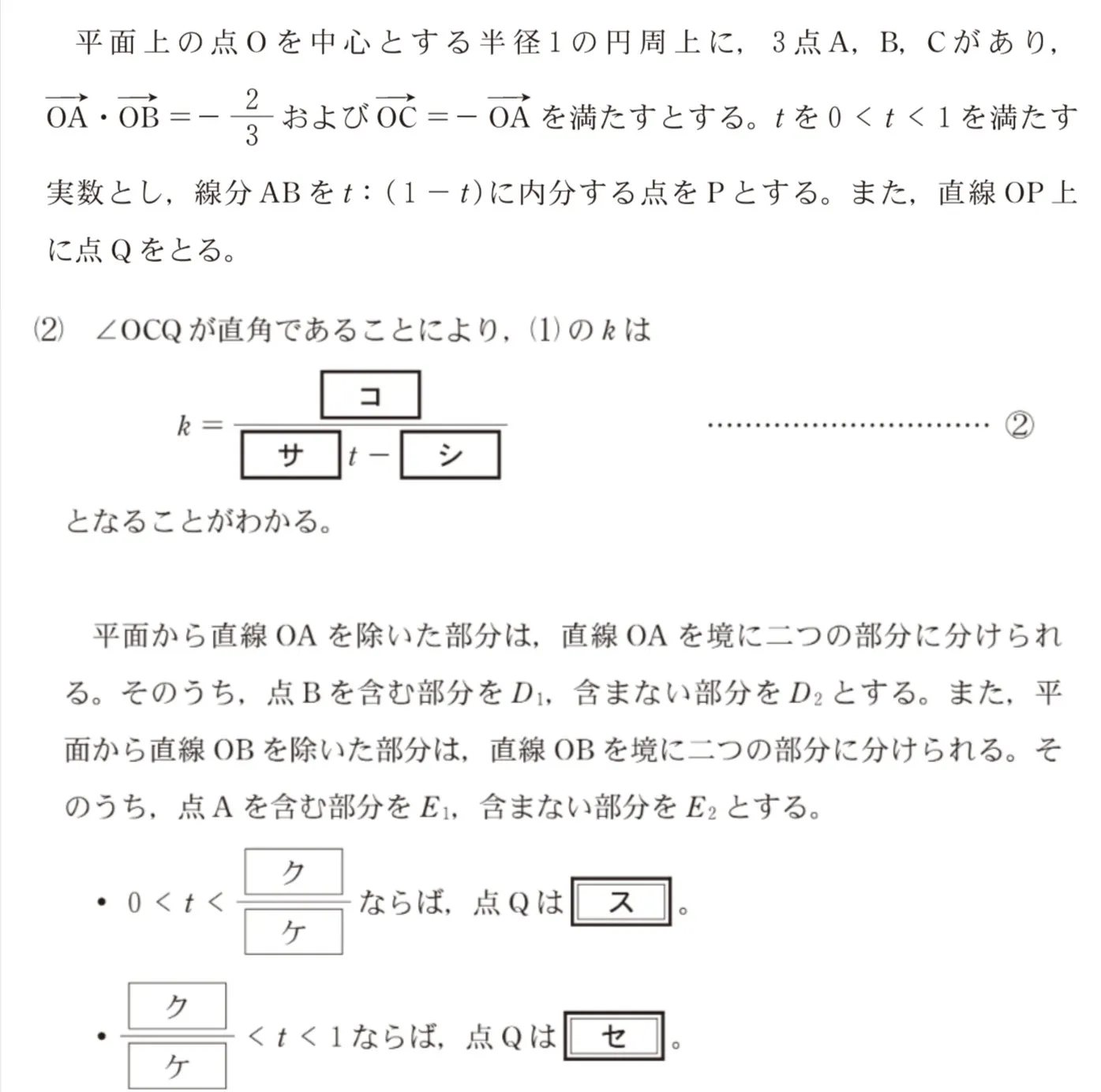
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)本試験 問113(数学Ⅱ・数学B(第5問) 問9) (訂正依頼・報告はこちら)

- D1に含まれ、かつE1に含まれる
- D1に含まれ、かつE2に含まれる
- D2に含まれ、かつE1に含まれる
- D2に含まれ、かつE2に含まれる
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
解答 セ: D1に含まれ、かつE1に含まれる
【表記に関する注意】
ここではベクトルを上に矢印をつけず右に添えて「OA→」などのように表記します。
簡潔な解説
まず②を①に代入して
(OQ→) = {3(1-t)/(5t-3)} (OA→) + {3t/(5t-3)} (OB→)
となります。3/5 < t < 1 のとき、
(OA→)の係数が正なので、QはAを含む側であるE1に含まれる
(OB→)の係数が正なので、QはBを含む側であるD1に含まれる
とわかります。よって答えは「D1に含まれ、かつE1に含まれる」となります。
詳細な解説
直前の問題(ス)と同様に考えます。
まず、スの解説の一部を引用します。
前問で求めた ク:3 ケ:5 を用います(解説は省略)。
3/5 < t < 1 のとき、「1-t > 0」と「5t-3 > 0」であることに注意して、
点Qのx座標について 3(1-t)/(5t-3) > 0 (正)
点Qのy座標について 3t/(5t-3) > 0 (正)
となるので、点Qは“第1象限”つまりD1かつE1の領域にあります。
よって答えは「セ: D1に含まれ、かつE1に含まれる」になります。
この選択肢が正解となります。
ここでは直交していない直線OAと直線OBをx軸とy軸のようにみなした座標平面を
考えました。このような考え方を斜交座標と言います。
もし今回の問題設定とは違ってOAとOBが直交していれば、
見慣れた直交座標になります。
参考になった数0
この解説の修正を提案する
02
(ス)と同様です。
この問題は、これまでの問題で分かったことを図に書くと下のようになります。
ここで、∠ACQ=90°より、直線CQは円の接線になります。
また、クケ<t<1なので、∠AOP>90°となるように図を書きます。
この図を見ると、QはD1かつE1の領域にあることがわかります。
QはD1かつE1の領域にあるので正解です。
QはD1かつE1の領域にあるので誤りです。
QはD1かつE1の領域にあるので誤りです。
QはD1かつE1の領域にあるので誤りです。
問題で与えられた条件をもとに図を書く必要があります。かなり複雑な図になるので、落ち着いて書いていきましょう。
参考になった数0
この解説の修正を提案する
前の問題(問112)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問114)へ