大学入学共通テスト（数学） 過去問
令和4年度（2022年度）追・再試験
問8 (数学Ⅰ・数学A（第1問） 問8)
問題文
以下（ サシ ）に当てはまるものを選べ。
以下の問題を解答するにあたっては、必要に応じて 三角比の表（リンク） を用いてもよい。
火災時に、ビルの高層階に取り残された人を救出する際、はしご車を使用することがある。
図1のはしご車で考える。はしごの先端をA、はしごの支点をBとする。はしごの角度（はしごと水平面のなす角の大きさ）は75°まで大きくすることができ、はしごの長さABは35mまで伸ばすことができる。また、はしごの支点Bは地面から2mの高さにあるとする。
以下、はしごの長さABは35mに固定して考える。また、はしごは太さを無視して線分とみなし、はしご車は水平な地面上にあるものとする。
（1）はしごの先端Aの最高到達点の高さは、地面から（ サシ ）mである。小数第1位を四捨五入して答えよ。
以下の問題を解答するにあたっては、必要に応じて 三角比の表（リンク） を用いてもよい。
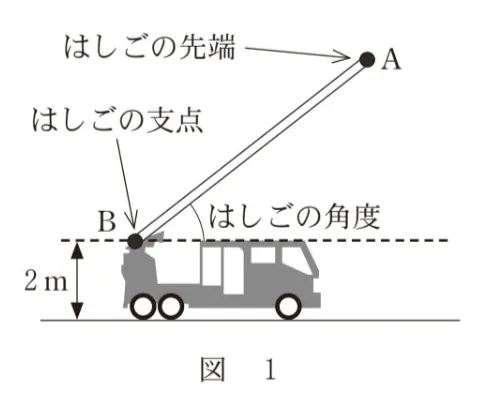
火災時に、ビルの高層階に取り残された人を救出する際、はしご車を使用することがある。
図1のはしご車で考える。はしごの先端をA、はしごの支点をBとする。はしごの角度（はしごと水平面のなす角の大きさ）は75°まで大きくすることができ、はしごの長さABは35mまで伸ばすことができる。また、はしごの支点Bは地面から2mの高さにあるとする。
以下、はしごの長さABは35mに固定して考える。また、はしごは太さを無視して線分とみなし、はしご車は水平な地面上にあるものとする。
（1）はしごの先端Aの最高到達点の高さは、地面から（ サシ ）mである。小数第1位を四捨五入して答えよ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和4年度（2022年度）追・再試験 問8（数学Ⅰ・数学A（第1問） 問8） （訂正依頼・報告はこちら）
以下（ サシ ）に当てはまるものを選べ。
以下の問題を解答するにあたっては、必要に応じて 三角比の表（リンク） を用いてもよい。
火災時に、ビルの高層階に取り残された人を救出する際、はしご車を使用することがある。
図1のはしご車で考える。はしごの先端をA、はしごの支点をBとする。はしごの角度（はしごと水平面のなす角の大きさ）は75°まで大きくすることができ、はしごの長さABは35mまで伸ばすことができる。また、はしごの支点Bは地面から2mの高さにあるとする。
以下、はしごの長さABは35mに固定して考える。また、はしごは太さを無視して線分とみなし、はしご車は水平な地面上にあるものとする。
（1）はしごの先端Aの最高到達点の高さは、地面から（ サシ ）mである。小数第1位を四捨五入して答えよ。
以下の問題を解答するにあたっては、必要に応じて 三角比の表（リンク） を用いてもよい。
火災時に、ビルの高層階に取り残された人を救出する際、はしご車を使用することがある。
図1のはしご車で考える。はしごの先端をA、はしごの支点をBとする。はしごの角度（はしごと水平面のなす角の大きさ）は75°まで大きくすることができ、はしごの長さABは35mまで伸ばすことができる。また、はしごの支点Bは地面から2mの高さにあるとする。
以下、はしごの長さABは35mに固定して考える。また、はしごは太さを無視して線分とみなし、はしご車は水平な地面上にあるものとする。
（1）はしごの先端Aの最高到達点の高さは、地面から（ サシ ）mである。小数第1位を四捨五入して答えよ。
- 36
- 37
- 38
- 39
正解！素晴らしいです
残念...
この過去問の解説 （2件）
01
解答 サシ: 36
解説
はしごの先端Aの最高到達点の高さが地面から何mなのかを求める問題です。
はしごの先端Aが最も高くなるのは角度が75°のときです。
三角比の表から sin 75° = 0.9659 を読み取っておきます。
2 + 35 sin 75° = 2 + 35・0.9659 = 2 + 33.8065 = 35.8065
よって答えは 36 m つまり サシ: 36 となります。
この選択肢が答えとなります。
注意
はしご車の高さ(2m)を足すのを忘れないように注意しましょう。
なお、問題設定から直ちに答えが37m未満であることがわかり、
選択肢のうちその条件を満たすのは「36」しかないので計算せずに
正解できてしまいますが、これはあくまでこのウェブサイトで4択形式に
改変しているからであり、もともとの共通テストでは穴埋め形式で出題された
問題ですので、練習のために正攻法で解くことをおすすめします。
参考になった数0
この解説の修正を提案する
02
はしごの先端Aが最も高くなる時は、はしごの角度は75°の時です。
もし仮に（この問題では起こり得ませんが）、はしごの角度が90°になった場合、はしごの地面からの高さは35+2=37mとなります。
よって、はしごの角度が75°の場合は必ず37mよりは小さくなります。
選択肢の中で37mより小さいものがこれしかないので、これが正解となります。
37m以上なので誤りです。
37m以上なので誤りです。
37m以上なので誤りです。
少し考えれば全く計算をする必要がない問題でした。
＜別解＞
はしごの角度が75°のとき、Aの高さは2+35sin(75°)となります。三角関数表からsin（75°）=0.9659なので、
2+35sin(75°)=2+35×0.9659=35.8065
よりAの高さは36m.
としてももちろん良いです。
参考になった数0
この解説の修正を提案する
前の問題（問7）へ
令和4年度（2022年度）追・再試験 問題一覧
次の問題（問9）へ