大学入学共通テスト(数学) 過去問
令和4年度(2022年度)追・再試験
問9 (数学Ⅰ・数学A(第1問) 問9)
問題文
以下の問題を解答するにあたっては、必要に応じて 三角比の表(リンク) を用いてもよい。
火災時に、ビルの高層階に取り残された人を救出する際、はしご車を使用することがある。
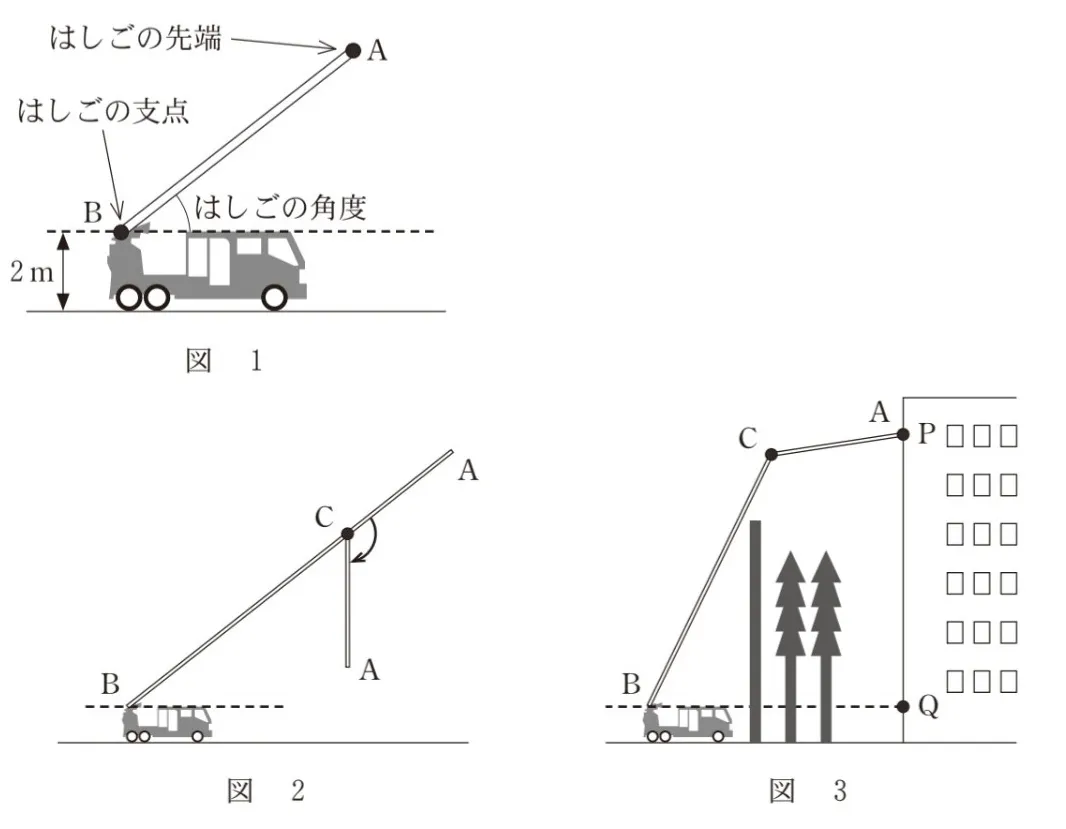
図1のはしご車で考える。はしごの先端をA、はしごの支点をBとする。はしごの角度(はしごと水平面のなす角の大きさ)は75°まで大きくすることができ、はしごの長さABは35mまで伸ばすことができる。また、はしごの支点Bは地面から2mの高さにあるとする。
以下、はしごの長さABは35mに固定して考える。また、はしごは太さを無視して線分とみなし、はしご車は水平な地面上にあるものとする。
(2)図1のはしごは、図2のように、点Cで、ACが鉛直方向になるまで下向きに屈折させることができる。ACの長さは10mである。
図3のように、あるビルにおいて、地面から26mの高さにある位置を点Pとする。
障害物のフェンスや木があるため、はしご車をBQの長さが18mとなる場所にとめる。ここで、点Qは、点Pの真下で、点Bと同じ高さにある位置である。
このとき、はしごの先端Aが点Pに届くかどうかは、障害物の高さや、はしご車と障害物の距離によって決まる。
そこで、このことについて、後の(ⅰ)のように考える。
ただし、はしご車、障害物、ビルは同じ水平な地面上にあり、点A、B、C、P、Qはすべて同一平面上にあるものとする。
(ⅰ)はしごを点Cで屈折させ、はしごの先端Aが点Pに一致したとすると、∠QBCの大きさはおよそ( ス )°になる。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)追・再試験 問9(数学Ⅰ・数学A(第1問) 問9) (訂正依頼・報告はこちら)
以下の問題を解答するにあたっては、必要に応じて 三角比の表(リンク) を用いてもよい。
火災時に、ビルの高層階に取り残された人を救出する際、はしご車を使用することがある。
図1のはしご車で考える。はしごの先端をA、はしごの支点をBとする。はしごの角度(はしごと水平面のなす角の大きさ)は75°まで大きくすることができ、はしごの長さABは35mまで伸ばすことができる。また、はしごの支点Bは地面から2mの高さにあるとする。
以下、はしごの長さABは35mに固定して考える。また、はしごは太さを無視して線分とみなし、はしご車は水平な地面上にあるものとする。
(2)図1のはしごは、図2のように、点Cで、ACが鉛直方向になるまで下向きに屈折させることができる。ACの長さは10mである。
図3のように、あるビルにおいて、地面から26mの高さにある位置を点Pとする。
障害物のフェンスや木があるため、はしご車をBQの長さが18mとなる場所にとめる。ここで、点Qは、点Pの真下で、点Bと同じ高さにある位置である。
このとき、はしごの先端Aが点Pに届くかどうかは、障害物の高さや、はしご車と障害物の距離によって決まる。
そこで、このことについて、後の(ⅰ)のように考える。
ただし、はしご車、障害物、ビルは同じ水平な地面上にあり、点A、B、C、P、Qはすべて同一平面上にあるものとする。
(ⅰ)はしごを点Cで屈折させ、はしごの先端Aが点Pに一致したとすると、∠QBCの大きさはおよそ( ス )°になる。

- 53
- 56
- 59
- 63
- 67
- 71
- 75
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
解答 ス: 71
解説
∠QBCのおよその大きさを求める問題です。
∠QBC = ∠QBA + ∠ABC として考えます。
準備としてまずABの長さを求めておきます。
AQ=PQ=26-2=24に注意します。
三角形ABQは直角三角形であり、三平方の定理より
AB = √(182 + 242) = 6 √(32 + 42) = 6 √25 = 30
あるいは 3 : 4 : 5 の直角三角形であることに気づけば
楽に AB = 30 が求まります。
∠QBAを求めましょう。正弦・余弦・正接のうちどれを用いても構いませんが、
たとえば余弦なら
cos ∠QBA = 3/5 = 0.6
となり、三角比の表から余弦の値が0.6に一番近いものを探すと、
cos 53° = 0.6018
が見つかります。よって∠QBAはおよそ53°です。
∠ABCを求めましょう。三角形ABCについて
AB : BC : CA = 30 : 25 :10 = 6 : 5 : 2
であるので、余弦定理より、
cos ∠ABC = (62 + 52 - 22)/(2・6・5)
= (36+25-4)/60 = 57/60 = 19/20 = 0.95
三角比の表から余弦の値が0.95に一番近いものを探すと、
cos 18° = 0.9511
が見つかります。よって∠ABCはおよそ18°です。
∠QBAはおよそ53°で、∠ABCはおよそ18°ですから、
∠QBC = ∠QBA + ∠ABC はおよそ71°ということになります。
よって答えは 71° つまり ス: 71 となります。
この選択肢が答えとなります。
「三角形の3辺の比がわかれば余弦定理で角度を求めることができる」
ということは押さえておきましょう。
参考になった数0
この解説の修正を提案する
02
まず問題文を図にしてみます。はしごが地面から2mのところにあるので、AQ=24mであることに注意してください。
方針としては、cosαとcosβから三角関数表を用いてαとβを求め、それらの和(α+β)の大きさを計算します。
まず△ABQは直角三角形で、cosα=18/30=3/5=0.6(三角関数表)より、およそα=53°です。
次に△ABCですが、余弦定理より、
102=252+303−2×25×30×cosβ
これを計算して、cosβ=0.95なので、およそβ=18°
よってαとβのだいたいの大きさがもとまったので、これらを足すと、
53+18=71
よりおよそ∠QBC=71°となります。
およそ、∠QBC=71°なので誤りです。
およそ、∠QBC=71°なので誤りです。
およそ、∠QBC=71°なので誤りです。
およそ、∠QBC=71°なので誤りです。
およそ、∠QBC=71°なので誤りです。
およそ、∠QBC=71°なので正解です。
およそ、∠QBC=71°なので誤りです。
角度を求めるときは、cosやsinに注目して求めることが多いです。
計算可能なαとβに四角形ACBQを分割するのが難しい問題です。
参考になった数0
この解説の修正を提案する
前の問題(問8)へ
令和4年度(2022年度)追・再試験 問題一覧
次の問題(問10)へ