大学入学共通テスト(数学) 過去問
令和5年度(2023年度)本試験
問36 (数学Ⅰ・数学A(第4問) 問4)
問題文
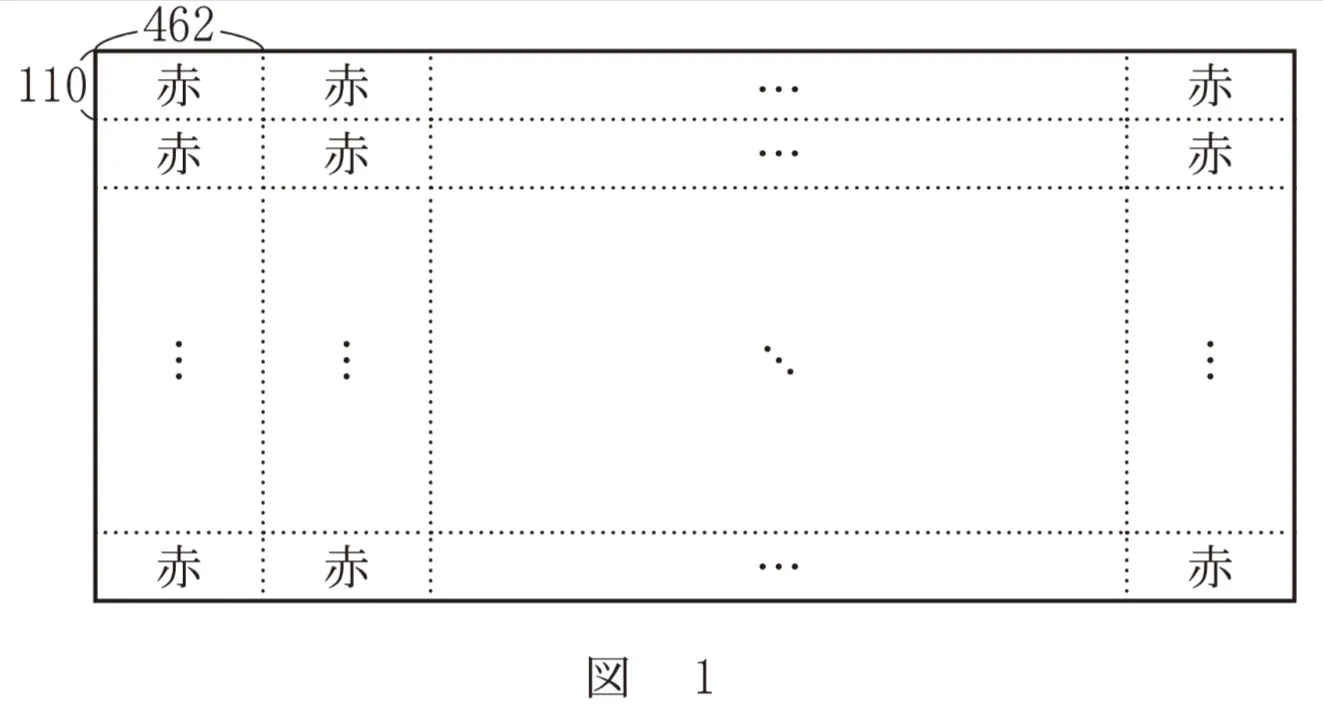
(1)横の長さが462で縦の長さが110である赤い長方形を、図1のように並べて正方形や長方形を作ることを考える。
462と110の両方を割り切る素数のうち最大のものは( アイ )である。
赤い長方形を並べて作ることができる正方形のうち、辺の長さが最小であるものは、一辺の長さが( ウエオカ )のものである。
また、赤い長方形を並べて正方形ではない長方形を作るとき、横の長さと縦の長さの差の絶対値が最小になるのは、462の約数と110の約数を考えると、差の絶対値が( キク )になるときであることがわかる。
縦の長さが横の長さより( キク )長い長方形のうち、横の長さが最小であるものは、横の長さが( ケコサシ )のものである。
( ケコサシ )にあてはまるものを次のうちから1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)本試験 問36(数学Ⅰ・数学A(第4問) 問4) (訂正依頼・報告はこちら)
(1)横の長さが462で縦の長さが110である赤い長方形を、図1のように並べて正方形や長方形を作ることを考える。
462と110の両方を割り切る素数のうち最大のものは( アイ )である。
赤い長方形を並べて作ることができる正方形のうち、辺の長さが最小であるものは、一辺の長さが( ウエオカ )のものである。
また、赤い長方形を並べて正方形ではない長方形を作るとき、横の長さと縦の長さの差の絶対値が最小になるのは、462の約数と110の約数を考えると、差の絶対値が( キク )になるときであることがわかる。
縦の長さが横の長さより( キク )長い長方形のうち、横の長さが最小であるものは、横の長さが( ケコサシ )のものである。
( ケコサシ )にあてはまるものを次のうちから1つ選べ。

- 1740
- 1748
- 1840
- 1848
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
前の問題(問35)で,( キク )が22であることを求めています。
本問では,このxとyを用いて解いていきます。
縦の長さが横の長さより22長い長方形なので,
110y-462x=22
両辺をー22で割って 21x-5y=-1 ……①
①を満たす自然数x,yの組のうち,xが最小であるものを考えていきます。
(x,y)=(-1,-4)は等式①を満たします。すなわち,
21×(-1)-5×(-4)=-1 ……②
①,②を辺々引いて
21(x+1)-5(y+4)=0
21(x+1)=5(y+4)
左辺は21の倍数,右辺は5の倍数で,両辺は等しいので,両辺は21と5の公倍数です。
21と5が互いに素であることから,21と5の公倍数は,整数kを用いて
21×5k
と表すことができます。よって
21(x+1)=5(y+4)=21×5k
21(x+1)=21×5k , 5(y+4)=21×5k
x+1=5k , y+4=21k
すなわち
x=5k-1 , y=21k―4 ……③
③において,k=1 のときx,yともに正で最小になります。
このとき x=5×1-1=4
横の長さは 462×4=1848
正解です。
不定方程式を変形して,xとyをそれぞれkの式で表す解法は,過去の共通テストでもしばしば出題されています。解き方,考え方をしっかり復習しておきましよう。
参考になった数0
この解説の修正を提案する
02
問題の意味を正しく読み取りましょう。誘導にうまく乗って前問の式を用いましょう。
前問より、|21a-5b|=1となる場合が、横と縦の差が22となります。今、横の長さが462a、縦の長さが110bであり、題意を満たすのは
462a-110b=-22、つまり21a-5b=-1を満たすときです。
よってこのときのa、bを求めればよく、a=4、b=17となります。
よって、このときの横の長さは、
462×4=1848となります。
参考になった数0
この解説の修正を提案する
前の問題(問35)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問37)へ