大学入学共通テスト(数学) 過去問
令和5年度(2023年度)本試験
問35 (数学Ⅰ・数学A(第4問) 問3)
問題文
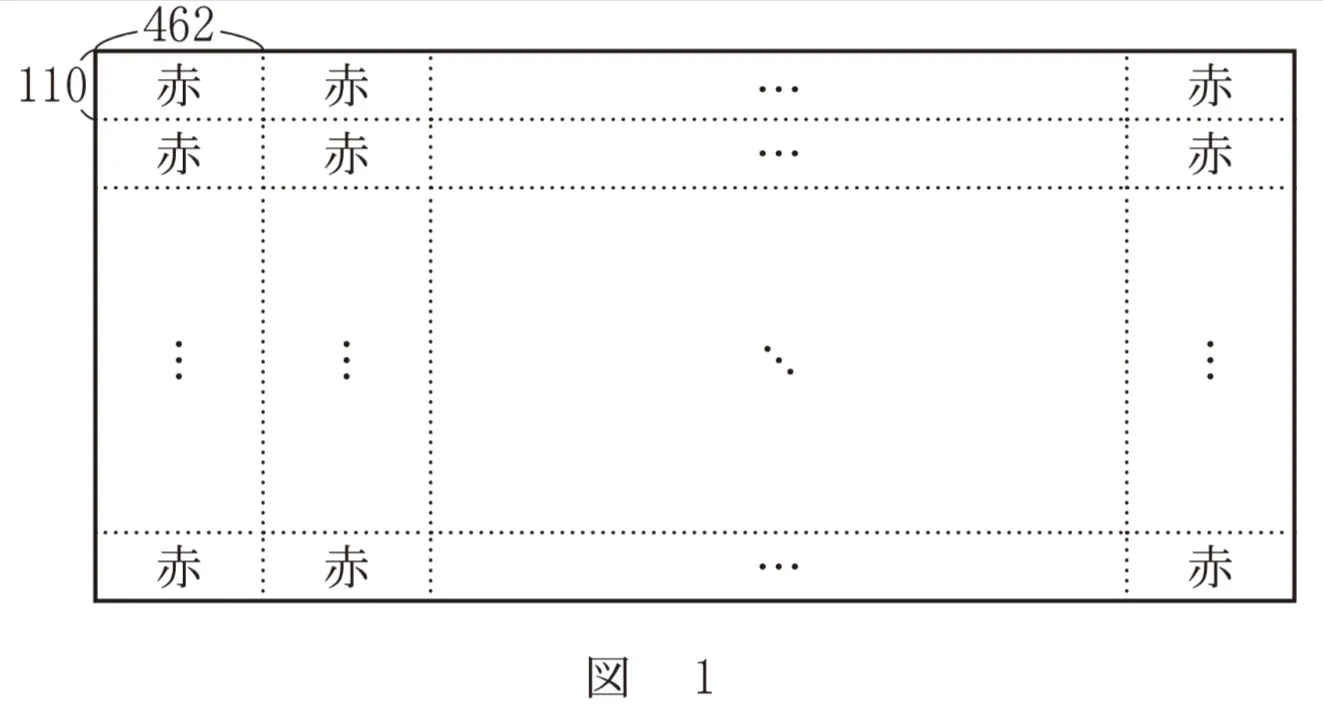
(1)横の長さが462で縦の長さが110である赤い長方形を、図1のように並べて正方形や長方形を作ることを考える。
462と110の両方を割り切る素数のうち最大のものは( アイ )である。
赤い長方形を並べて作ることができる正方形のうち、辺の長さが最小であるものは、一辺の長さが( ウエオカ )のものである。
また、赤い長方形を並べて正方形ではない長方形を作るとき、横の長さと縦の長さの差の絶対値が最小になるのは、462の約数と110の約数を考えると、差の絶対値が( キク )になるときであることがわかる。
縦の長さが横の長さより( キク )長い長方形のうち、横の長さが最小であるものは、横の長さが( ケコサシ )のものである。
( キク )にあてはまるものを次のうちから1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)本試験 問35(数学Ⅰ・数学A(第4問) 問3) (訂正依頼・報告はこちら)
(1)横の長さが462で縦の長さが110である赤い長方形を、図1のように並べて正方形や長方形を作ることを考える。
462と110の両方を割り切る素数のうち最大のものは( アイ )である。
赤い長方形を並べて作ることができる正方形のうち、辺の長さが最小であるものは、一辺の長さが( ウエオカ )のものである。
また、赤い長方形を並べて正方形ではない長方形を作るとき、横の長さと縦の長さの差の絶対値が最小になるのは、462の約数と110の約数を考えると、差の絶対値が( キク )になるときであることがわかる。
縦の長さが横の長さより( キク )長い長方形のうち、横の長さが最小であるものは、横の長さが( ケコサシ )のものである。
( キク )にあてはまるものを次のうちから1つ選べ。

- 21
- 22
- 23
- 24
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
x,yを自然数として,赤い長方形を横にx個,縦にy個並べて長方形を作るとします。
横の長さは462x,縦の長さは110yとなりますから,その差は
462x-110y=22(21x-5y)
となります。
また,正方形ではない長方形を作るときですから,横の長さと縦の長さの差は0ではありません。すなわち,
21x-5y≠0
さらに,x=1,y=4のとき21x-5y=1 となりますから,21x-5yの絶対値の最小値は1です。
したがって,横の長さと縦の長さの差22(21x-5y)の絶対値が最小になるのは,差の絶対値が22になるときです。
正解です。
2つの整数a,bが互いに素であるとき,不定方程式
ax+by=1
は,必ず整数解をもちます。
したがって,
21x-5y=1
も,必ず整数解をもちます。
ただし,自然数の解があるとは限りませんので,解説の中ではxとyに具体的な自然数を代入して,式の値が1になる場合があることを示しています。
参考になった数0
この解説の修正を提案する
02
約数に注目して、絶対値を考えていきましょう。
赤い正方形を横にa個、縦にb個並べることを考えます。前問の素因数分解の結果から、
|462a-110b|
=|(2×3×7×11)a-(2×5×11)b|
=2×11|21a-5b| となります。
これが最小の自然数になるのは、|21a-5b|が最小となるときです。(0ではない)
よって|21a-5b|=1となる、a=1、b=4が見つかります。これより、
2×11×1=22が最小の自然数です。
参考になった数0
この解説の修正を提案する
前の問題(問34)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問36)へ