大学入学共通テスト（数学）過去問
令和5年度（2023年度）追・再試験
問80 (数学Ⅱ・数学B（第2問）問13)

問題文

（　ノ　）・（　ハ　）にあてはまるものを1つ選べ。

1²＋2²＋…＋10²をある関数の定積分で表すことを考えよう。問題文の画像

付箋

付箋は自分だけが見れます（非公開です）。

このページは閲覧用ページです。
履歴を残すには、「新しく出題する（ここをクリック）」をご利用ください。

問題

大学入学共通テスト（数学）試験令和5年度（2023年度）追・再試験問80（数学Ⅱ・数学B（第2問）問13）（訂正依頼・報告はこちら）

（　ノ　）・（　ハ　）にあてはまるものを1つ選べ。

1²＋2²＋…＋10²をある関数の定積分で表すことを考えよう。

正解！素晴らしいです

残念...

ツテの回答
∫_t^t+1xdx=[x²/2]_t^t+1
=(t+1)²/2-t²/2
=(2t+1)/2
=t+1/2

トナの回答
∫_t^t+1x²dx=[x³/3]_t^t+1
=(t+1)³/3-t³/3
=(t³+3t²+3t+1-t³)/3
=(3t²+3t+1)/3
=t²+t+1/3

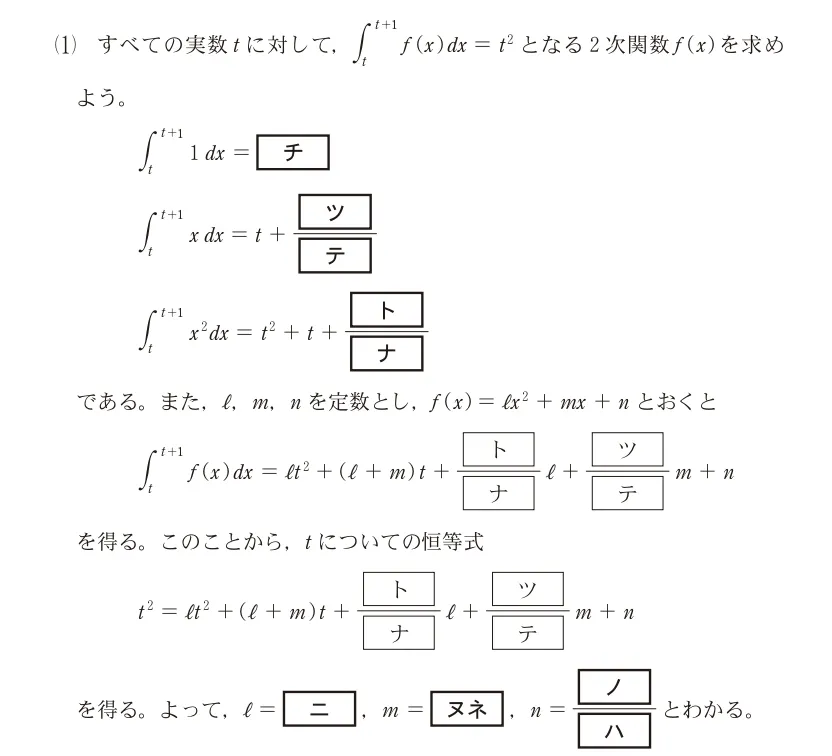
tについての恒等式は、

t²=lt²+(l+m)t+l/3+m/2+n

なので、

l=1・・・①

l+m=0・・・②

l/3+m/2+n=0・・・③

①を②に代入して

m=-1

①とm=-1を③に代入して

1/3-1/2+n=0

n=1/6

選択肢3. ノ：1　　ハ：6

正解です。

参考になった数0