共通テスト（数学） 過去問
令和6年度（2024年度）本試験
問35 (数学Ⅰ・数学A（第4問） 問2)
問題文
T3、T4、T6を次のようなタイマーとする。
T3：3進数を3桁表示するタイマー
T4：4進数を3桁表示するタイマー
T6：6進数を3桁表示するタイマー
なお、n進数とはn進法で表された数のことである。
これらのタイマーは、すべて次の表示方法に従うものとする。
＜表示方法＞
（a）スタートした時点でタイマーは000と表示されている。
（b）タイマーは、スタートした後、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻る。
（c）タイマーは表示が000に戻った後も、（b）と同様に、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻るという動作を繰り返す。
例えば、T3はスタートしてから3進数で12（3）秒後に012と表示される。その後、222と表示された1秒後に表示が000に戻り、その12（3）秒後に再び012と表示される。
（1）T6は、スタートしてから10進数で40秒後に（ アイウ ）と表示される。T4は、スタートしてから2進数で10011（2）秒後に（ エオカ ）と表示される。
（ エオカ ）にあてはまるものを1つ選べ。
T3：3進数を3桁表示するタイマー
T4：4進数を3桁表示するタイマー
T6：6進数を3桁表示するタイマー
なお、n進数とはn進法で表された数のことである。
これらのタイマーは、すべて次の表示方法に従うものとする。
＜表示方法＞
（a）スタートした時点でタイマーは000と表示されている。
（b）タイマーは、スタートした後、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻る。
（c）タイマーは表示が000に戻った後も、（b）と同様に、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻るという動作を繰り返す。
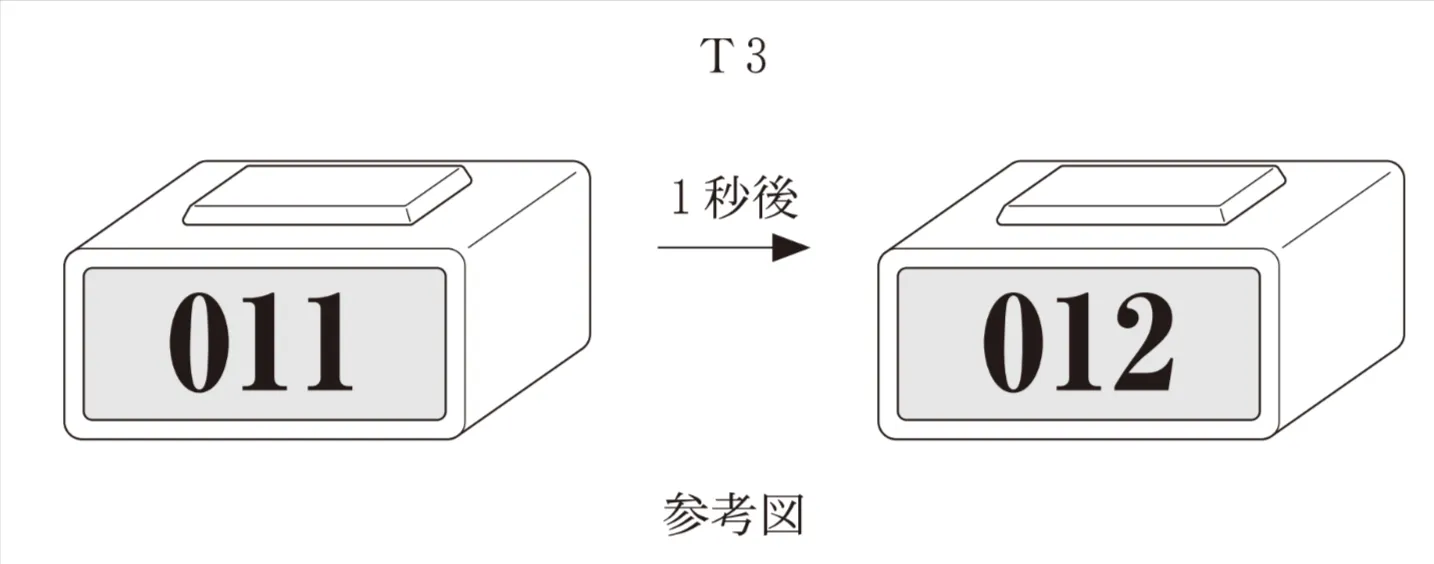
例えば、T3はスタートしてから3進数で12（3）秒後に012と表示される。その後、222と表示された1秒後に表示が000に戻り、その12（3）秒後に再び012と表示される。
（1）T6は、スタートしてから10進数で40秒後に（ アイウ ）と表示される。T4は、スタートしてから2進数で10011（2）秒後に（ エオカ ）と表示される。
（ エオカ ）にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
共通テスト（数学）試験 令和6年度（2024年度）本試験 問35（数学Ⅰ・数学A（第4問） 問2） （訂正依頼・報告はこちら）
T3、T4、T6を次のようなタイマーとする。
T3：3進数を3桁表示するタイマー
T4：4進数を3桁表示するタイマー
T6：6進数を3桁表示するタイマー
なお、n進数とはn進法で表された数のことである。
これらのタイマーは、すべて次の表示方法に従うものとする。
＜表示方法＞
（a）スタートした時点でタイマーは000と表示されている。
（b）タイマーは、スタートした後、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻る。
（c）タイマーは表示が000に戻った後も、（b）と同様に、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻るという動作を繰り返す。
例えば、T3はスタートしてから3進数で12（3）秒後に012と表示される。その後、222と表示された1秒後に表示が000に戻り、その12（3）秒後に再び012と表示される。
（1）T6は、スタートしてから10進数で40秒後に（ アイウ ）と表示される。T4は、スタートしてから2進数で10011（2）秒後に（ エオカ ）と表示される。
（ エオカ ）にあてはまるものを1つ選べ。
T3：3進数を3桁表示するタイマー
T4：4進数を3桁表示するタイマー
T6：6進数を3桁表示するタイマー
なお、n進数とはn進法で表された数のことである。
これらのタイマーは、すべて次の表示方法に従うものとする。
＜表示方法＞
（a）スタートした時点でタイマーは000と表示されている。
（b）タイマーは、スタートした後、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻る。
（c）タイマーは表示が000に戻った後も、（b）と同様に、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻るという動作を繰り返す。
例えば、T3はスタートしてから3進数で12（3）秒後に012と表示される。その後、222と表示された1秒後に表示が000に戻り、その12（3）秒後に再び012と表示される。
（1）T6は、スタートしてから10進数で40秒後に（ アイウ ）と表示される。T4は、スタートしてから2進数で10011（2）秒後に（ エオカ ）と表示される。
（ エオカ ）にあてはまるものを1つ選べ。
- 103
- 104
- 105
- 106
正解！素晴らしいです
残念...
この過去問の解説 （3件）
01
2進数の10011を10進数で表すと、
24 +21 +1 =42 +3
= 1・42 + 0・41 + 3 なので、
4進数では 103 になります。
「103」の選択肢が設問（エオカ）の解答となります。
進数の10011 の1桁めと2桁めの合計は10進数では3であり、
それは4進数でも同じであるため、
本設問に限って言えば1桁めが 3 である事からこの選択肢を直ちに選ぶ事も可能です。
ただしそれはチェック用に考えて、普通に計算するほうがよいでしょう。
10進数で例えば3023は 3・103 +0・102 +2・101 + 3 となります。
同様にして2進数と4進数について考えています。
2進数の10011を10進数にして、
その後で4進数ではどうなるかを考えています。
上記解説では 24 = 42 (= 16) の計算も使いました。
4進数では各桁の数値が3以下にしかならないため、
1桁めに「4」が入っているこの選択肢は誤りになります。
同様に「105」「106」の選択肢も誤りになり消去法が使えますが、
チェック用に使えると考えたほうがよいでしょう。
解き方は1通りではありませんが、
上記解説では式の中で「桁」がどのような意味を持つかを考えた方法を使いました。
2進数のn桁めが 1 の時、それは10進数では2n-1を表します。
本設問での2進数での 10011 の5桁めは10進数では24を表します。
同様に2桁めの 1 は10進数で 21 =2 を表し、
1桁めの 1 は10進数でも同じく 1 を表します。
参考になった数0
この解説の修正を提案する
02
２進数で表された10011を４進数に変換します。
まず、２進数の10011を10進数に変換します。次に、10進数を４進数に直します。
10011（２）を10進数に変換します。以下のようにそれぞれの桁に重みがあるので、それを足していきます。
次に、19（10）を4進数に変換していきます。
よって、エオカ 103 となります。
参考になった数0
この解説の修正を提案する
03
T4タイマーがスタートしてから2進数で10011(2)秒後の表示を考えます。
まず、経過時間である2進数の10011(2)を、計算しやすい10進数に変換します。
n進数を10進数に変換するには、各桁の数に、その桁の「重み」を掛けて全て足し合わせます。
10011(2)の各桁の重みは、右から順に20、21、22、23、24となります。
したがって、10進数に変換すると次のようになります。
1*24+0*23+0*22+1*21+1*20
=1*16+0*8+0*4+1*2+1*1
=16+0+0+2+1
=19
つまり、10011(2)秒後というのは、10進数で19秒後のことです。
次に、この10進数の「19」を、T4タイマーの表示である4進数に変換します。
10進数をn進数に変換するには、その数をnで繰り返し割り、その余りを逆から並べる方法が有効です。
19/4=4･･･3
4/4=1･･･0
1/4=0･･･1
出てきた余りを下から順番に並べると、「103」となります。
参考になった数0
この解説の修正を提案する
前の問題（問34）へ
令和6年度（2024年度）本試験 問題一覧
次の問題（問36）へ