大学入学共通テスト(数学) 過去問
令和6年度(2024年度)本試験
問36 (数学Ⅰ・数学A(第4問) 問3)
問題文
T3:3進数を3桁表示するタイマー
T4:4進数を3桁表示するタイマー
T6:6進数を3桁表示するタイマー
なお、n進数とはn進法で表された数のことである。
これらのタイマーは、すべて次の表示方法に従うものとする。
<表示方法>
(a)スタートした時点でタイマーは000と表示されている。
(b)タイマーは、スタートした後、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻る。
(c)タイマーは表示が000に戻った後も、(b)と同様に、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻るという動作を繰り返す。
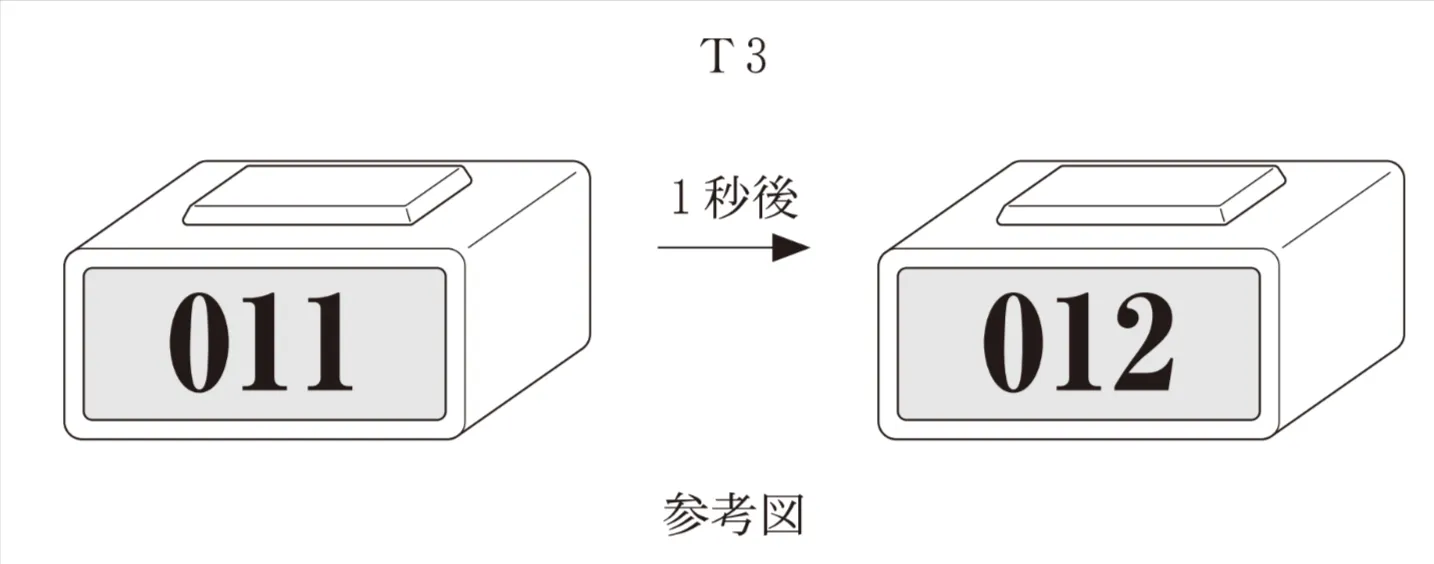
例えば、T3はスタートしてから3進数で12(3)秒後に012と表示される。その後、222と表示された1秒後に表示が000に戻り、その12(3)秒後に再び012と表示される。
(2)T4をスタートさせた後、初めて表示が000に戻るのは、スタートしてから10進数で( キク )秒後であり、その後も( キク )秒ごとに表示が000に戻る。
同様の考察をT6に対しても行うことにより、T4とT6を同時にスタートさせた後、初めて両方の表示が同時に000に戻るのは、スタートしてから10進数で( ケコサシ )秒後であることがわかる。
( キク )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)本試験 問36(数学Ⅰ・数学A(第4問) 問3) (訂正依頼・報告はこちら)
T3:3進数を3桁表示するタイマー
T4:4進数を3桁表示するタイマー
T6:6進数を3桁表示するタイマー
なお、n進数とはn進法で表された数のことである。
これらのタイマーは、すべて次の表示方法に従うものとする。
<表示方法>
(a)スタートした時点でタイマーは000と表示されている。
(b)タイマーは、スタートした後、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻る。
(c)タイマーは表示が000に戻った後も、(b)と同様に、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻るという動作を繰り返す。
例えば、T3はスタートしてから3進数で12(3)秒後に012と表示される。その後、222と表示された1秒後に表示が000に戻り、その12(3)秒後に再び012と表示される。
(2)T4をスタートさせた後、初めて表示が000に戻るのは、スタートしてから10進数で( キク )秒後であり、その後も( キク )秒ごとに表示が000に戻る。
同様の考察をT6に対しても行うことにより、T4とT6を同時にスタートさせた後、初めて両方の表示が同時に000に戻るのは、スタートしてから10進数で( ケコサシ )秒後であることがわかる。
( キク )にあてはまるものを1つ選べ。

- 63
- 64
- 65
- 66
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
T4は4進数を3桁で表示するタイマーです。
これは、各位で使える数字が0、1、2、3の4種類であることを意味します。
3桁で表示できる数の組み合わせの総数は、
百の位が4通り、
十の位が4通り、
一の位が4通りあるため、
全部で4*4*4=64通りとなります。
タイマーは000からスタートし、1秒ごとに数が1ずつ増えていき、64個の数をすべて表示し終えると、再び000に戻ります。
したがって、T4が初めて表示が000に戻るのは、スタートしてから64秒後です。
参考になった数0
この解説の修正を提案する
前の問題(問35)へ
令和6年度(2024年度)本試験 問題一覧
次の問題(問37)へ