共通テスト（数学）過去問
令和6年度（2024年度）本試験
問37 (数学Ⅰ・数学A（第4問）問4)

問題文

T3、T4、T6を次のようなタイマーとする。
　T3：3進数を3桁表示するタイマー
　T4：4進数を3桁表示するタイマー
　T6：6進数を3桁表示するタイマー
なお、n進数とはn進法で表された数のことである。
これらのタイマーは、すべて次の表示方法に従うものとする。

＜表示方法＞
（a）スタートした時点でタイマーは000と表示されている。
（b）タイマーは、スタートした後、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻る。
（c）タイマーは表示が000に戻った後も、（b）と同様に、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻るという動作を繰り返す。

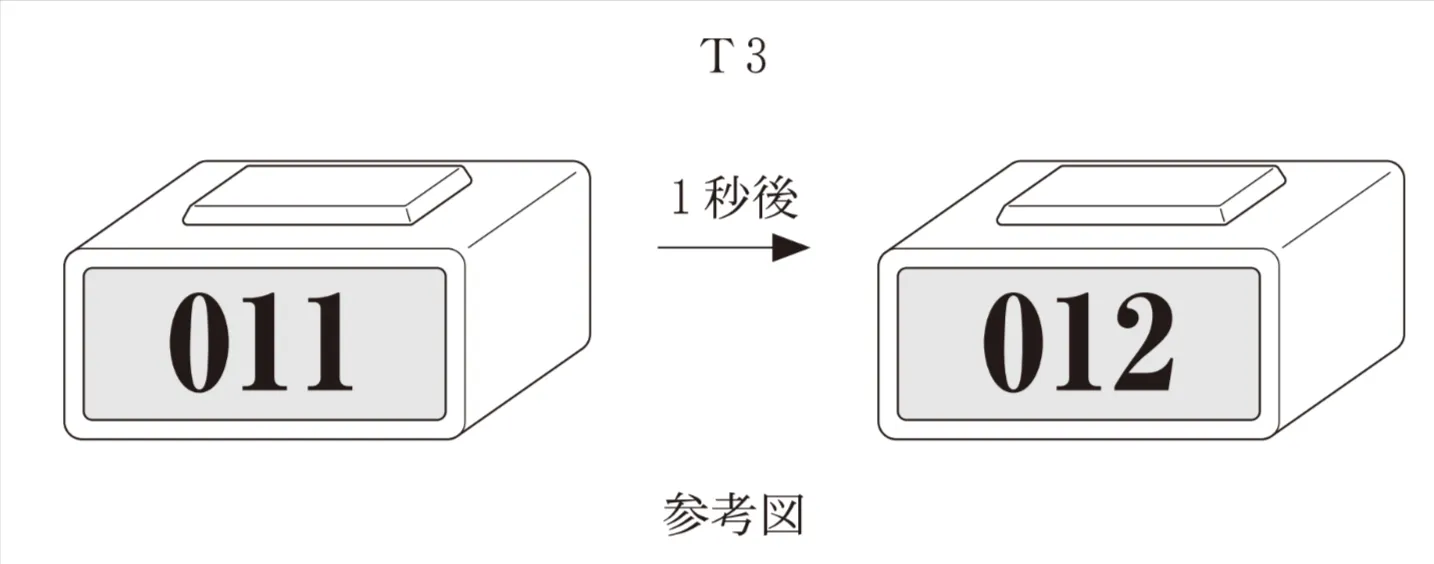
例えば、T3はスタートしてから3進数で12_（3）秒後に012と表示される。その後、222と表示された1秒後に表示が000に戻り、その12_（3）秒後に再び012と表示される。

（2）T4をスタートさせた後、初めて表示が000に戻るのは、スタートしてから10進数で（　キク　）秒後であり、その後も（　キク　）秒ごとに表示が000に戻る。
同様の考察をT6に対しても行うことにより、T4とT6を同時にスタートさせた後、初めて両方の表示が同時に000に戻るのは、スタートしてから10進数で（　ケコサシ　）秒後であることがわかる。

（　ケコサシ　）にあてはまるものを1つ選べ。問題文の画像

付箋

イエロー
グリーン
ブルー
レッド

付箋は自分だけが見れます（非公開です）。

このページは閲覧用ページです。
履歴を残すには、「新しく出題する（ここをクリック）」をご利用ください。

問題

共通テスト（数学）試験令和6年度（2024年度）本試験問37（数学Ⅰ・数学A（第4問）問4）（訂正依頼・報告はこちら）

1428
1528
1628
1728

正解！素晴らしいです

残念...

この過去問の解説（3件）

4 と 6 の最小公倍数が 12 であるので、
12 進数で考えたときに「タイマー」が 000 に戻るような条件を考えます。

12進数での「タイマー」の最大値は、
11・12²+ 11・12¹ + 11 = 11・144 + 132 +11
= 1584 + 143 = 1727
その「1秒後」に「タイマー」は 000 となるので、
求める値は 1727 + 1 = 1728 です。

「1728」の選択肢が設問（ケコサシ）の解答となります。

選択肢4. 1728

設問（キク）の結果より4進数が 000 に戻る時刻が分かっているので、
6進数で同様の値を求めてから最小公倍数を考えても同じ結果を得ます。
(5・6² + 5・6¹ + 5) + 1 = 180 + 30 + 5 +1 = 216 であり、
216 = 3・72 = 27・4・2 です。
他方、

64 = 4³であるため、

216・(4・2) = 1728 (= 64・27) が求める値となります。

設問（キク）

4進数での「タイマー」の最大値を10進数で表すと、
3・4² + 3・4¹ + 3 = 48 + 12 + 3 = 63
問題文より「その1秒後にタイマーは 000 に戻る」ので、
その時刻は10進数で 63 + 1 = 64 秒後です。

まとめ

12進数で考えたときに「タイマー」が 000 に戻るとき、
4進数で考えたときと6進数で考えたときの「タイマー」も 000 に戻る事になります。
(11・12²+ 11・12¹ + 11) +1 は
8・{(5・6² + 5・6¹ + 5) + 1} と同じ値であり、
27・{(3・4² + 3・4¹ + 3) + 1} と同じ値でもあります。
本設問では問われていませんが、
「6進数のタイマー」は8周し、
「4進数のタイマー」は27周した時に、
開始時刻を1回めとして2回目に同時に 000 となります。