大学入学共通テスト(数学) 過去問
令和6年度(2024年度)本試験
問39 (数学Ⅰ・数学A(第4問) 問6)
問題文
T3:3進数を3桁表示するタイマー
T4:4進数を3桁表示するタイマー
T6:6進数を3桁表示するタイマー
なお、n進数とはn進法で表された数のことである。
これらのタイマーは、すべて次の表示方法に従うものとする。
<表示方法>
(a)スタートした時点でタイマーは000と表示されている。
(b)タイマーは、スタートした後、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻る。
(c)タイマーは表示が000に戻った後も、(b)と同様に、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻るという動作を繰り返す。
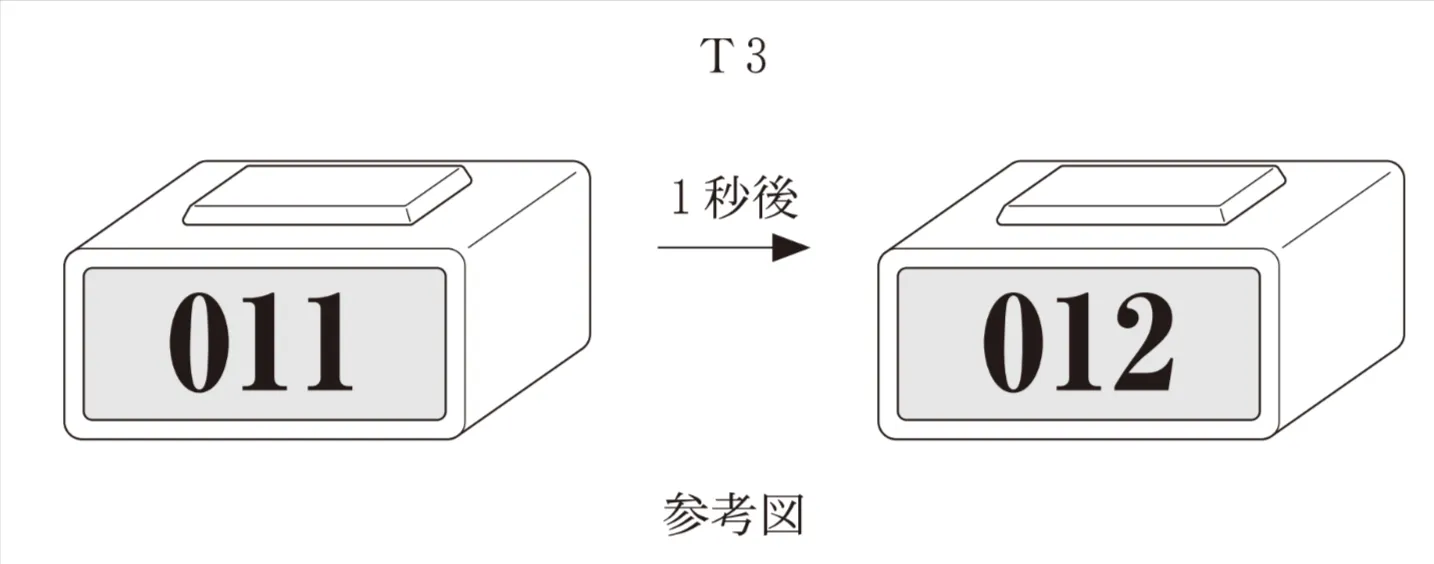
例えば、T3はスタートしてから3進数で12(3)秒後に012と表示される。その後、222と表示された1秒後に表示が000に戻り、その12(3)秒後に再び012と表示される。
(3)0以上の整数lに対して、T4をスタートさせたl秒後にT4が012と表示されることと
lを( スセ )で割った余りが( ソ )であること
は同値である。ただし、( スセ )と( ソ )は10進法で表されているものとする。
T3についても同様の考察を行うことにより、次のことがわかる。
T3とT4を同時にスタートさせてから、初めて両方が同時に012と表示されるまでの時間をm秒とするとき、mは10進法で( タチツ )と表される。
また、T4とT6の表示に関する記述として、正しいものは( テ )である。
( タチツ )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)本試験 問39(数学Ⅰ・数学A(第4問) 問6) (訂正依頼・報告はこちら)
T3:3進数を3桁表示するタイマー
T4:4進数を3桁表示するタイマー
T6:6進数を3桁表示するタイマー
なお、n進数とはn進法で表された数のことである。
これらのタイマーは、すべて次の表示方法に従うものとする。
<表示方法>
(a)スタートした時点でタイマーは000と表示されている。
(b)タイマーは、スタートした後、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻る。
(c)タイマーは表示が000に戻った後も、(b)と同様に、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻るという動作を繰り返す。
例えば、T3はスタートしてから3進数で12(3)秒後に012と表示される。その後、222と表示された1秒後に表示が000に戻り、その12(3)秒後に再び012と表示される。
(3)0以上の整数lに対して、T4をスタートさせたl秒後にT4が012と表示されることと
lを( スセ )で割った余りが( ソ )であること
は同値である。ただし、( スセ )と( ソ )は10進法で表されているものとする。
T3についても同様の考察を行うことにより、次のことがわかる。
T3とT4を同時にスタートさせてから、初めて両方が同時に012と表示されるまでの時間をm秒とするとき、mは10進法で( タチツ )と表される。
また、T4とT6の表示に関する記述として、正しいものは( テ )である。
( タチツ )にあてはまるものを1つ選べ。

- 418
- 518
- 628
- 728
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
T3とT4が同時に012と表示されるまでの時間mを求めます。
まず、T3について考えます。
T3は3進数を3桁で表示するので、最大の数は222(3)です。
222(3)を10進数に変換すると、
222(3)
=2*32+2*31+2*30
=2*9+2*3+2*1
=18+6+2
=26
よって、T3の周期は26+1=27秒です。
T3が012と表示するのは、012(3)を10進数に変換した時間なので、
012(3)
=0*32+1*31+2*30
=0+3+2
=5
つまり、T3が012と表示される時間mは、27で割った余りが5である必要があります。
これを合同式で表すとm≡5(mod27)となります。
一方、T4が012と表示される時間mは、以下の考察から、mを64で割った余りが6である必要があります。
合同式で表すとm≡6(mod64)となります。
求める時間mは、これら2つの合同式を同時に満たす最小の正の整数です。
m=27k+5(kは0以上の整数)
m=64j+6(jは0以上の整数)
と表せるので、
27k+5=64j+6
27k-64j=1
という一次不定方程式を解きます。
ユークリッドの互除法を用いて特殊解を求めると、
64=2*27+10
27=2*10+7
10=1*7+3
7=2*3+1
これを逆にたどっていくと、
1=7-2*3
=7-2*(10-7)=3*7-2*10
=3*(27-2*10)-2*10=3*27-8*10
=3*27-8*(64-2*27)=19*27-8*64
よって、27*19-64*8=1が成り立ち、特殊解の一つとして(k,j)=(19,8)が見つかります。
これをmの式に代入すると、
m=27*19+5=513+5=518
m=64*8+6=512+6=518
k,jが最小の正の整数となる場合を考えると、このm=518が初めて同時に表示される時間となります。
参考になった数0
この解説の修正を提案する
前の問題(問38)へ
令和6年度(2024年度)本試験 問題一覧
次の問題(問40)へ