共通テスト（数学）過去問
令和6年度（2024年度）本試験
問43 (数学Ⅰ・数学A（第5問）問3)

問題文

図1のように、平面上に5点A、B、C、D、Eがあり、線分AC、CE、EB、BD、DAによって、星形の図形ができるときを考える。線分ACとBEの交点をP、ACとBDの交点をQ、BDとCEの交点をR、ADとCEの交点をS、ADとBEの交点をTとする。

ここでは
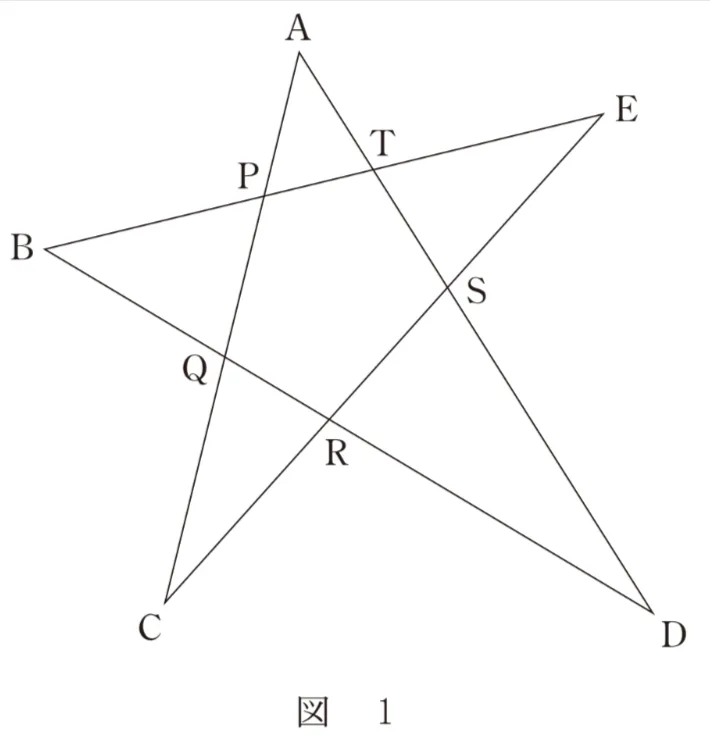
AP：PQ：QC＝2：3：3、　AT：TS：SD＝1：1：3
を満たす星形の図形を考える。
以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。

（1）ΔAQDと直線CEに着目すると

（QR／RD）・（DS／SA）・（［　ア　］／CQ）＝1

が成り立つので

QR：RD＝（　イ　）：（　ウ　）

となる。また、ΔAQDと直線BEに着目すると

QB：BD＝（　エ　）：（　オ　）

となる。したがって

BQ：QR：RD＝（　エ　）：（　イ　）：（　ウ　）

となることがわかる。

（　エ　）、（　オ　）にあてはまるものを1つ選べ。問題文の画像

付箋

イエロー
グリーン
ブルー
レッド

付箋は自分だけが見れます（非公開です）。

このページは閲覧用ページです。
履歴を残すには、「新しく出題する（ここをクリック）」をご利用ください。

問題

共通テスト（数学）試験令和6年度（2024年度）本試験問43（数学Ⅰ・数学A（第5問）問3）（訂正依頼・報告はこちら）

エ：2　　オ：6
エ：2　　オ：7
エ：3　　オ：5
エ：3　　オ：8

正解！素晴らしいです

残念...

この過去問の解説（3件）

（※問題文同様に、線分ACの長さをACと記します。）
求める比が QB:BD である事もヒントにして、
三角形AQDの辺DQを延長した場合のメネラウスの定理を考えます。
その時にメネラウスの定理により、
(BD/BQ)・(QP/PA)・(AT/TD) = 1
問題文の条件より、
QP/PA = 3/2
AT/TD = 1/(1 + 3) = 1/4
これらより、
BD/BQ = (2/3)・4 = 8/3
よって、QB:BD = BQ:BD = 3:8

エ：3　オ：8　の組み合わせの選択肢が本設問の解答となります。

選択肢4. エ：3　　オ：8

設問（ア）に引き続き、再びメネラウスの定理を使用します。
本設問では辺DQを延長した場合です。
延長した先の点がBとなります。

QP/PA と AT/TD を求める箇所は問題文の条件の比を使います。
すなわち、
AP:PQ:QC = 2:3:3
AT:TS:SD = 1:1:3 の条件を使います。

設問（ア）でのメネラウスの定理の適用は、

(QR/RD)・(DS/SA)・(AC/CQ) = 1 でした。

本設問では、

(BD/BQ)・(QP/PA)・(AT/TD) = 1 です。

三角形の辺で延長する箇所が異なります。

（分母と分子を全て入れ替えても同じように式が成立します。）

まとめ

星形の図形でやや分かりにくいと思われますが、
再びメネラウスの定理を適用し、
その後で問題文の条件も使い、 BD/BQ (=BD/QB) を求めます。

もしメネラウスの定理を部分的に忘れてしまった場合は、

設問（ア）によって内容を思い出せるかもしれません。

しかし定理を完全に忘れてしまっていた場合や、定理を知らなかった場合は本設問で行き詰まってしまう可能性があります。

メネラウスの定理、チェバの定理、方べきの定理などをよく確認するとともに、問題を多く解いて使い方に慣れましょう。

設問（ア）のまとめより（参考：メネラウスの定理の証明）
本設問での記号を使うと、線分CSに平行で点Qを通る直線を引きます。
その直線と線分ADの交点を新たにZとします。
すると、三角形の相似関係より次の2式が成立します。
AC/CQ = SA/ZS
DS/RD = ZS/QR
すると、
(QR/RD)・(DS/SA)・(AC/CQ)
= (DS/RD)・(QR/SA)・(AC/CQ)
= (ZS/QR)・(QR/SA)・(SA/ZS)
= 1 が成立します。
（ZS, QR, SA がそれぞれ分母と分子で打ち消し合います。）