大学入学共通テスト(数学) 過去問
令和6年度(2024年度)本試験
問45 (数学Ⅰ・数学A(第5問) 問5)
問題文
ここでは
AP:PQ:QC=2:3:3、 AT:TS:SD=1:1:3
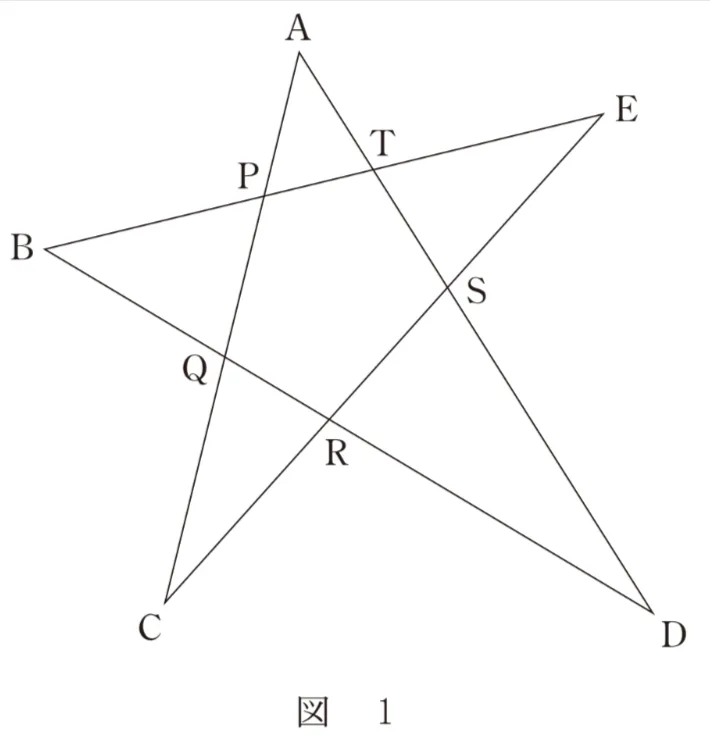
を満たす星形の図形を考える。
以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。
(2)5点P、Q、R、S、Tが同一円周上にあるとし、AC=8であるとする。
(ⅱ)3点A、B、Cを通る円と点Dとの位置関係を、次の構想に基づいて調べよう。
<構想>
線分ACとBDの交点Qに着目し、AQ・CQとBQ・DQの大小を比べる。
まず、AQ・CQ=5・3=15かつBQ・DQ=( キク )であるから
AQ・CQ( ケ )BQ・DQ ・・・・・①
が成り立つ。また、3点A、B、Cを通る円と直線BDとの交点のうち、Bと異なる点をXとすると
AQ・CQ( コ )BQ・XQ ・・・・・②
が成り立つ。①と②の左辺は同じなので、①と②の右辺を比べることにより、XQ( サ )DQが得られる。したがって、点Dは3点A、B、Cを通る円の( シ )にある。
( キク )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)本試験 問45(数学Ⅰ・数学A(第5問) 問5) (訂正依頼・報告はこちら)
ここでは
AP:PQ:QC=2:3:3、 AT:TS:SD=1:1:3
を満たす星形の図形を考える。
以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。
(2)5点P、Q、R、S、Tが同一円周上にあるとし、AC=8であるとする。
(ⅱ)3点A、B、Cを通る円と点Dとの位置関係を、次の構想に基づいて調べよう。
<構想>
線分ACとBDの交点Qに着目し、AQ・CQとBQ・DQの大小を比べる。
まず、AQ・CQ=5・3=15かつBQ・DQ=( キク )であるから
AQ・CQ( ケ )BQ・DQ ・・・・・①
が成り立つ。また、3点A、B、Cを通る円と直線BDとの交点のうち、Bと異なる点をXとすると
AQ・CQ( コ )BQ・XQ ・・・・・②
が成り立つ。①と②の左辺は同じなので、①と②の右辺を比べることにより、XQ( サ )DQが得られる。したがって、点Dは3点A、B、Cを通る円の( シ )にある。
( キク )にあてはまるものを1つ選べ。

- 45
- 46
- 47
- 48
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
この問題は、星形図形に内接する円の性質を利用して、線分の長さの積を求める問題です。
方べきの定理とメネラウスの定理を段階的に適用することで、答えを導き出すことができます。
条件より、AC=8であり、AP:PQ:QC=2:3:3です。
線分ACの比の合計は2+3+3=8なので、それぞれの長さは以下のようになります。
AP=(2/8)*8=2
PQ=(3/8)*8=3
QC=(3/8)*8=3
したがって、AQの長さはAP+PQ=2+3=5となります。
次に、「5点P、Q、R、S、Tが同一円周上にある」という条件に着目します。
この5点を通る円を考えると、点Aは、この円の2つの弦PQとTSを含む直線(それぞれ直線ACと直線AD)の交点です。
したがって、点Aについて方べきの定理が成り立ちます。
AT*AS=AP*AQ
AT*AS=2*5=10
ここで、AT:TS:SD=1:1:3より
AT=kとおくと、TS=k、SD=3kとなります。
AS=AT+TS=k+k=2kです。
これを方べきの定理の式に代入すると、
k*(2k)=10
2k2=10
k2=5
k=√5
よって、AT=√5、TS=√5、SD=3√5となります。
この結果から、AS=2√5、AD=5√5、TD=TS+SD=4√5であることが分かります。
続いて、点Dについて同様に方べきの定理を考えます。
点Dは、円の2つの弦QRとSTを含む直線(それぞれ直線BDと直線AD)の交点です。
したがって、方べきの定理より、
DQ*DR=DS*DT
DS=3√5、DT=TS+SD=√5+3√5=4√5なので、
DQ*DR=(3√5)*(4√5)=12*5=60
となります。
次に、線分BQとDQの比を求めるために、メネラウスの定理を利用します。
△ADQと、その3辺(または延長線)を切る直線BPEに着目します。
メネラウスの定理より、
(AT/TD)*(DB/BQ)*(QP/PA)=1
(√5/4√5)*(DB/BQ)*(3/2)=1
(1/4)*(DB/BQ)*(3/2)=1
(3/8)*(DB/BQ)=1
DB/BQ=8/3
DB=BQ+QDなので、(BQ+QD)/BQ=8/3となり、
1+(QD/BQ)=8/3
QD/BQ=5/3
よって、BQ:QD=3:5という関係が分かります。
BQ=3m,DQ=5mとおくと、
BQ*DQ=15m2
今度は、△ADQと、その3辺(または延長線)を切る直線CREに着目します。
メネラウスの定理より、
(AC/CQ)*(QR/RD)*(DS/SA)=1
(8/3)*(QR/RD)*(3√5/2√5)=1
(8/3)*(QR/RD)*(3/2)=1
4*(QR/RD)=1
RD=4QR
QD=QR+RDであるため、RD=4QRを代入すると、
QD=QR+4QR=5QR
となり、QR=(1/5)QD、RD=(4/5)QD
この関係を、DQ*DR=60に代入します。
DQ*((4/5)QD)=60
(4/5)DQ2=60
DQ2=60*(5/4)=75
よって
BQ=(3/5)DQとなるため
BQ*DQ
=(3/5)DQ*DQ
=(3/5)DQ2
BQ*DQ=(3/5)*75=45
となります。
参考になった数0
この解説の修正を提案する
前の問題(問44)へ
令和6年度(2024年度)本試験 問題一覧
次の問題(問46)へ