大学入学共通テスト(数学) 過去問
令和6年度(2024年度)本試験
問50 (数学Ⅰ・数学A(第5問) 問10)
問題文
ここでは
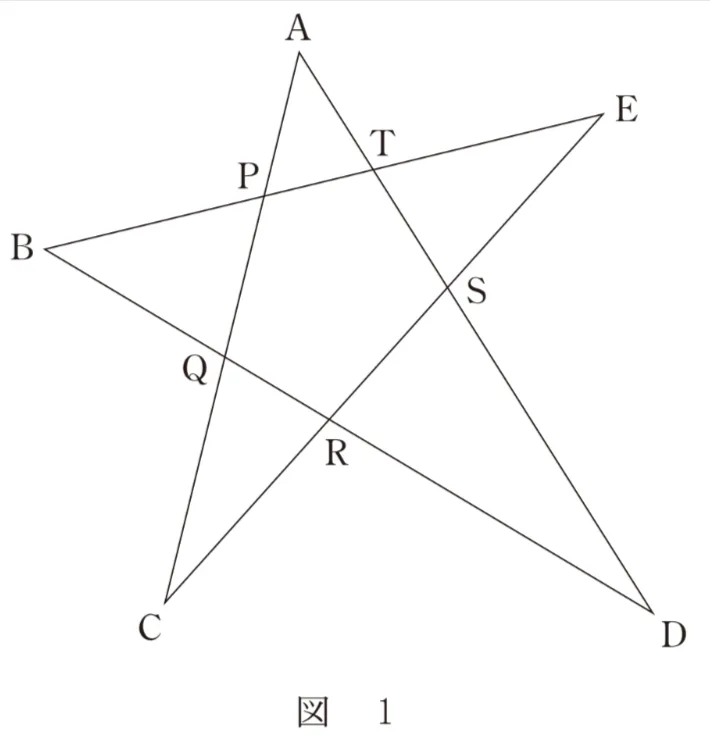
AP:PQ:QC=2:3:3、 AT:TS:SD=1:1:3
を満たす星形の図形を考える。
以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。
(2)5点P、Q、R、S、Tが同一円周上にあるとし、AC=8であるとする。
(ⅲ)3点C、D、Eを通る円と2点A、Bとの位置関係について調べよう。
この星形の図形において、さらにCR=RS=SE=3となることがわかる。したがって、点Aは3点C、D、Eを通る円の( ス )にあり、点Bは3点C、D、Eを通る円の( セ )にある。
( ス )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)本試験 問50(数学Ⅰ・数学A(第5問) 問10) (訂正依頼・報告はこちら)
ここでは
AP:PQ:QC=2:3:3、 AT:TS:SD=1:1:3
を満たす星形の図形を考える。
以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。
(2)5点P、Q、R、S、Tが同一円周上にあるとし、AC=8であるとする。
(ⅲ)3点C、D、Eを通る円と2点A、Bとの位置関係について調べよう。
この星形の図形において、さらにCR=RS=SE=3となることがわかる。したがって、点Aは3点C、D、Eを通る円の( ス )にあり、点Bは3点C、D、Eを通る円の( セ )にある。
( ス )にあてはまるものを1つ選べ。

- 内部
- 周上
- 外部
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
点Aが3点C,D,Eを通る円(以下、円CDEと呼びます)のどの位置にあるかを考えます。
点の位置関係を調べるには、その点を通り円と2点で交わる直線を考え、方べきの定理の考え方を利用します。
点Aを通り、円CDEと点Dで交わる直線ADに着目します。
ここで、直線ADと直線CEの交点Sを利用します。
点Sは、問題文の条件「CR=RS=SE=3」から、円CDEの弦である線分CE上の点です。
弦上の点は必ず円の内部にあるので、点Sは円CDEの内部にあります。
点Sに関して方べきの定理を考えると、
(SからCまでの距離)*(SからEまでの距離)と、
(SからDまでの距離)*(Sから、直線ADと円CDEが交わるもう一つの点D'までの距離)
の積は等しくなります。
問題文の条件から、SC=RS+CR=3+3=6、SE=3です。
よって、方べきの値(の絶対値)はSC*SE=6*3=18となります。
次に、直線AD上の長さについて考えます。
5点P,Q,R,S,Tが同一円周上にあるという条件から、この円に関する方べきの定理が使えます。
点Aは、直線PQと直線STの交点と見なせるので、
AP*AQ=AT*AS
が成り立ちます。
AC=8でAP:PQ:QC=2:3:3なので、
AP
=8*(2/(2+3+3))
=2
AQ
=AP+PQ
=2+(8*(3/8))
=5
よって、
AP*AQ=2*5=10
です。
AT:TS:SD=1:1:3なので、AT=xとおくと、TS=x,SD=3xとなります。
AS
=AT+TS
=2x
です。
AT*AS
=x*(2x)
=2x2
となります。
したがって、2x2=10より、x=√5と求まります。
これにより、各線分の長さが
AT=√5,TS=√5,SD=3*√5=3√5,AS=2√5
となります。
ここで、
SD*SD'=18であり、SD=3√5なので、
SD'
=18/(3√5)
=6/√5となります。
点Sは円の内部にあるため、点D'は、Sを基準としてDとは反対側にあります。
直線AD上の点の位置関係を、Sを基準に考えます。
点Aは、Sから見てDとは反対側にあり、その距離はAS=2√5です。
点D'も、Sから見てDとは反対側にあり、その距離はSD'=6/√5です。
ここで、ASとSD'の長さを比べると、
AS
=2√5
=10/√5
SD'=6/√5
となり、AS>SD'であることがわかります。
つまり、直線AD上では、点はA-D'-S-Dの順に並んでいます。
点Aは、円CDEと直線ADの交点であるDとD'を結ぶ線分D'Dの外側にあります。
したがって、点Aは円CDEの外部にあることがわかります。
参考になった数0
この解説の修正を提案する
前の問題(問49)へ
令和6年度(2024年度)本試験 問題一覧
次の問題(問51)へ