大学入学共通テスト（数学） 過去問
令和6年度（2024年度）追・試験
問86 (数学Ⅱ・数学B（第3問） 問3)
問題文
以下（ エ ）、（ オ ）にあてはまるものを1つ選べ。
以下の問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。
太郎さんと花子さんは、「はい」か「いいえ」のどちらかで答えられる質問を考えている。質問数は一つで、確率pで「はい」の回答が得られ、確率1−pで「いいえ」の回答が得られるものとする。この質問を、三人からなるグループの一人ひとりに別々に示し、そのうち一人だけが「はい」と回答する確率を考えたい。
以下の問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。
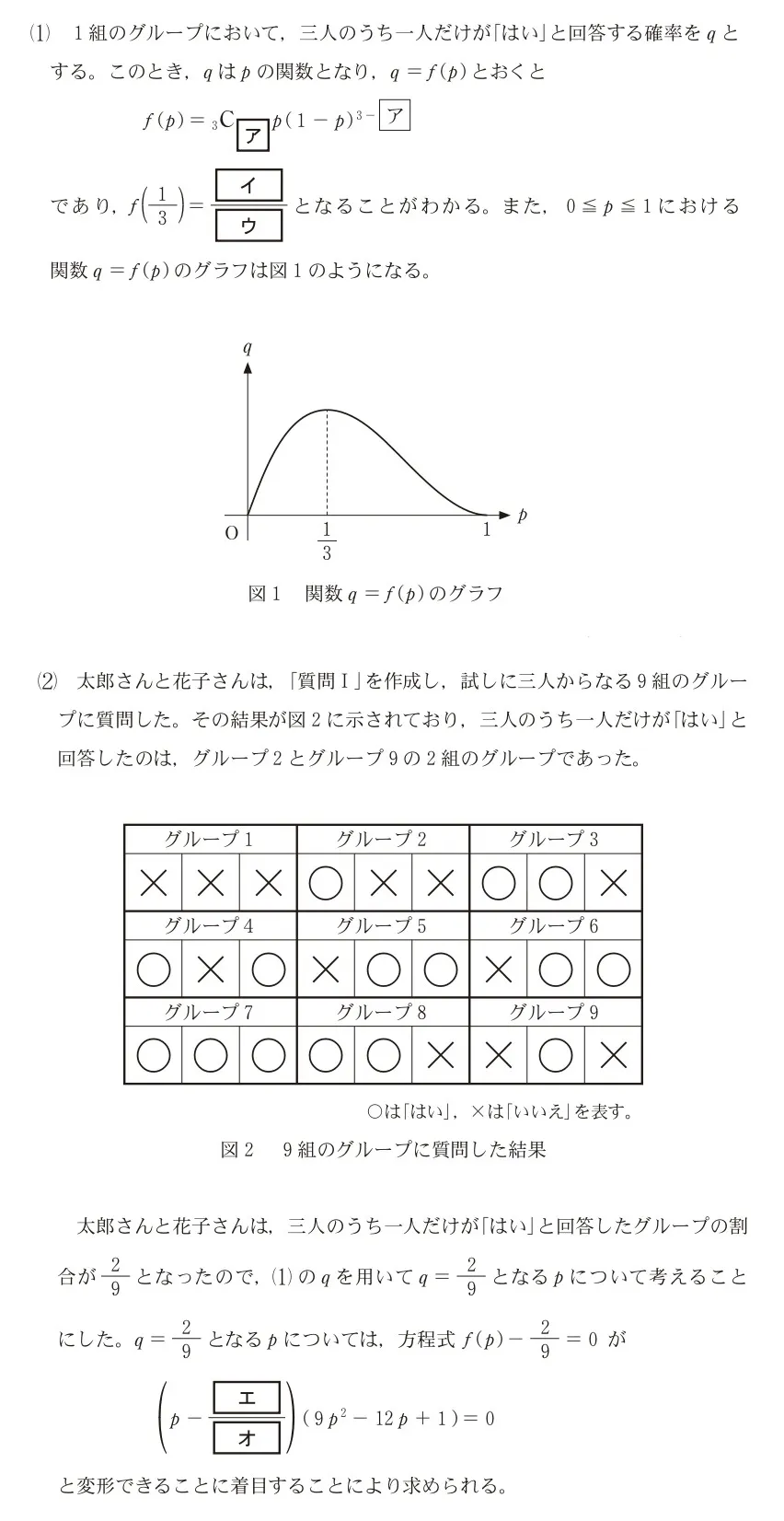
太郎さんと花子さんは、「はい」か「いいえ」のどちらかで答えられる質問を考えている。質問数は一つで、確率pで「はい」の回答が得られ、確率1−pで「いいえ」の回答が得られるものとする。この質問を、三人からなるグループの一人ひとりに別々に示し、そのうち一人だけが「はい」と回答する確率を考えたい。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和6年度（2024年度）追・試験 問86（数学Ⅱ・数学B（第3問） 問3） （訂正依頼・報告はこちら）
以下（ エ ）、（ オ ）にあてはまるものを1つ選べ。
以下の問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。
太郎さんと花子さんは、「はい」か「いいえ」のどちらかで答えられる質問を考えている。質問数は一つで、確率pで「はい」の回答が得られ、確率1−pで「いいえ」の回答が得られるものとする。この質問を、三人からなるグループの一人ひとりに別々に示し、そのうち一人だけが「はい」と回答する確率を考えたい。
以下の問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。
太郎さんと花子さんは、「はい」か「いいえ」のどちらかで答えられる質問を考えている。質問数は一つで、確率pで「はい」の回答が得られ、確率1−pで「いいえ」の回答が得られるものとする。この質問を、三人からなるグループの一人ひとりに別々に示し、そのうち一人だけが「はい」と回答する確率を考えたい。
- エ：1 オ：2
- エ：2 オ：3
- エ：3 オ：4
- エ：4 オ：5
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
反復試行の確率となるので
となります。
f(1/3)を解くと
f(1/3)=4/9
となります。
題意より
f(p)-2/9=0
と
(p-エ/オ)(9p2-12p+1)=0
が等しくなります。
ここで
f(p)-2/9=0
↔3p(1-p)2-2/9=0
ここで、p3項は3倍されていることから、定数項2/9も同様に3倍したらいいことが分かります。
従って(p-2/3)(9p2-12p+1)=0
正解です。
全て展開してもいいですが、その場合は時間をみてハマらないようにすることが大切です。
今回のように、比で解けるpointを念のためピックアップしました。
参考になった数0
この解説の修正を提案する
前の問題（問85）へ
令和6年度（2024年度）追・試験 問題一覧
次の問題（問87）へ