大学入学共通テスト(数学) 過去問
令和6年度(2024年度)追・試験
問94 (数学Ⅱ・数学B(第4問) 問4)
問題文
y=2x ・・・・・①
y=mx+4 ・・・・・②
を考える。
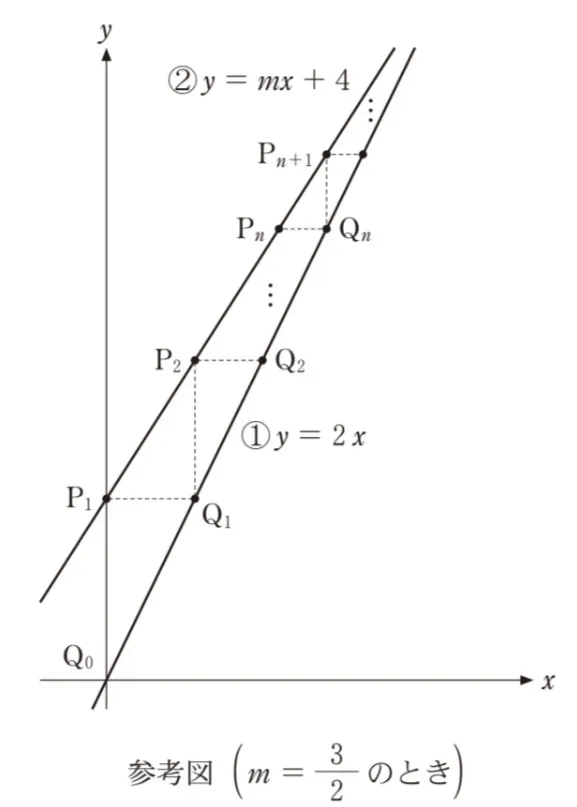
原点(0,0)をQ0、点(0,4)をP1とし、次の手順で点Q1、P2、Q2、…、Pn、Qn、Pn+1、…を定める。
<手順>
・P1からx軸に平行な直線を引いて、直線①との交点をQ1とする。
・Q1からy軸に平行な直線を引いて、直線②との交点をP2とする。
・・・
・Pnからx軸に平行な直線を引いて、直線①との交点をQnとする。
・Qnからy軸に平行な直線を引いて、直線②との交点をPn+1とする。
・・・
(1)m=2とする。すなわち、②はy=2x+4である。Q1の座標は([ ア ],[ イ ])であり、P2の座標は([ ウ ],[ エ ])である。
自然数nについて、Pnのy座標をanとする。Qnのx座標をanを用いて表すと、( オ )となる。よって、Pn+1のy座標an+1は( カ )となる。したがって、数列{an}の一般項はan=( キ )である。
( カ )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)追・試験 問94(数学Ⅱ・数学B(第4問) 問4) (訂正依頼・報告はこちら)
y=2x ・・・・・①
y=mx+4 ・・・・・②
を考える。
原点(0,0)をQ0、点(0,4)をP1とし、次の手順で点Q1、P2、Q2、…、Pn、Qn、Pn+1、…を定める。
<手順>
・P1からx軸に平行な直線を引いて、直線①との交点をQ1とする。
・Q1からy軸に平行な直線を引いて、直線②との交点をP2とする。
・・・
・Pnからx軸に平行な直線を引いて、直線①との交点をQnとする。
・Qnからy軸に平行な直線を引いて、直線②との交点をPn+1とする。
・・・
(1)m=2とする。すなわち、②はy=2x+4である。Q1の座標は([ ア ],[ イ ])であり、P2の座標は([ ウ ],[ エ ])である。
自然数nについて、Pnのy座標をanとする。Qnのx座標をanを用いて表すと、( オ )となる。よって、Pn+1のy座標an+1は( カ )となる。したがって、数列{an}の一般項はan=( キ )である。
( カ )にあてはまるものを1つ選べ。

- 2an
- an−2
- (1/2)an
- (1/2)an−2
- 2an−4
- 2an+4
- 3an−4
- an+4
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
便宜上、点Qn(Qnx,Qny)と表現いたします。
条件より、P1y=Q1yだから
4=2Q1x
↔Q1x=2
従ってQ1(2,4)
条件より、Q1x=P2xだから
P2y=2×2+4=8
従ってP2(2,8)
題意より、
Pn(Pnx,an)と表記できます。
このとき
Qn(Qnx,an)であるからy=2xに代入すると
an=2Qnx
従ってQnx=an/2
前問より
Pn((an-4)/2,an)
Qn(an/2,an)
と整理できPn+1は
Pn+1x=Qnx=an/2だから
y=2x+4より
Pn+1y=2×an/2+4=an+4
不正解です。
不正解です。
不正解です。
不正解です。
不正解です。
不正解です。
不正解です。
正解です。
1つずつ代入していくことが大切です。
参考になった数0
この解説の修正を提案する
前の問題(問93)へ
令和6年度(2024年度)追・試験 問題一覧
次の問題(問95)へ