大学入学共通テスト（数学） 過去問
令和6年度（2024年度）追・試験
問101 (数学Ⅱ・数学B（第5問） 問1)
問題文
以下（ ア ）にあてはまるものを1つ選べ。
平面上に3点O、A、Bがある。ただし、O、A、Bは同一直線上にはないとする。
平面上に3点O、A、Bがある。ただし、O、A、Bは同一直線上にはないとする。
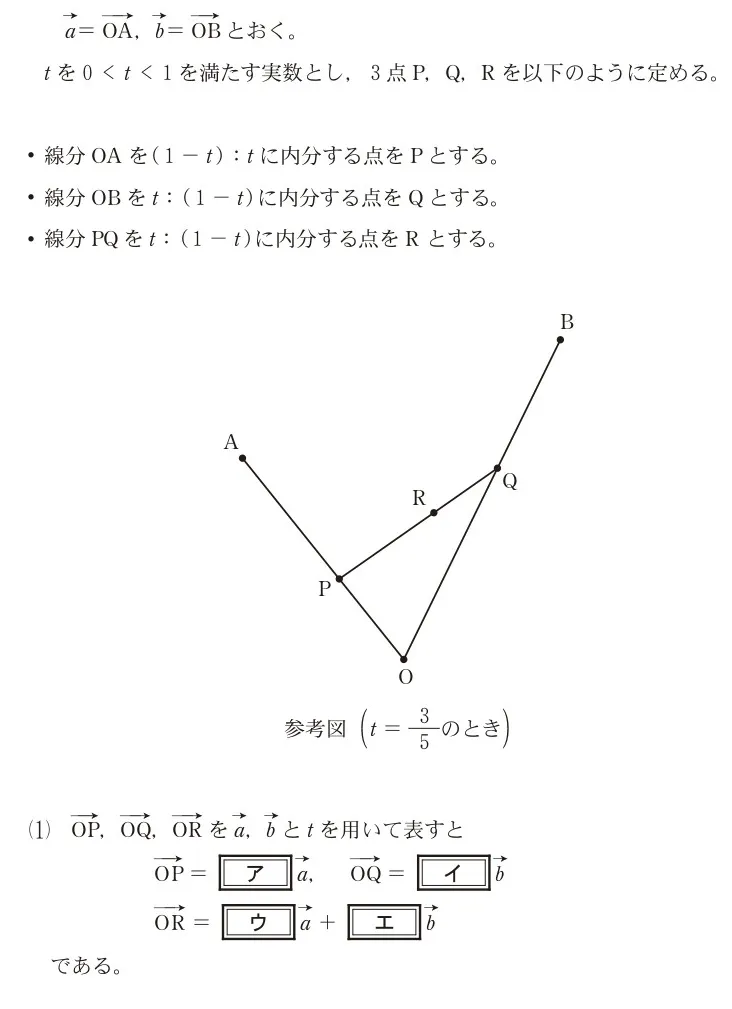
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和6年度（2024年度）追・試験 問101（数学Ⅱ・数学B（第5問） 問1） （訂正依頼・報告はこちら）
以下（ ア ）にあてはまるものを1つ選べ。
平面上に3点O、A、Bがある。ただし、O、A、Bは同一直線上にはないとする。
平面上に3点O、A、Bがある。ただし、O、A、Bは同一直線上にはないとする。
- t
- （t−1）
- （1−t）
- （−t）
- t2
- t（1−t）
- 2t（1−t）
- （1−t）2
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
PはOAを(1-t)：tに内分する点だから
不正解です。
不正解です。
正解です。
不正解です。
不正解です。
不正解です。
不正解です。
不正解です。
内分点など用語は復習しておくことが大事です。
参考になった数0
この解説の修正を提案する
前の問題（問100）へ
令和6年度（2024年度）追・試験 問題一覧
次の問題（問102）へ