大学入学共通テスト(数学) 過去問
令和6年度(2024年度)追・試験
問110 (数学Ⅱ・数学B(第5問) 問10)
問題文
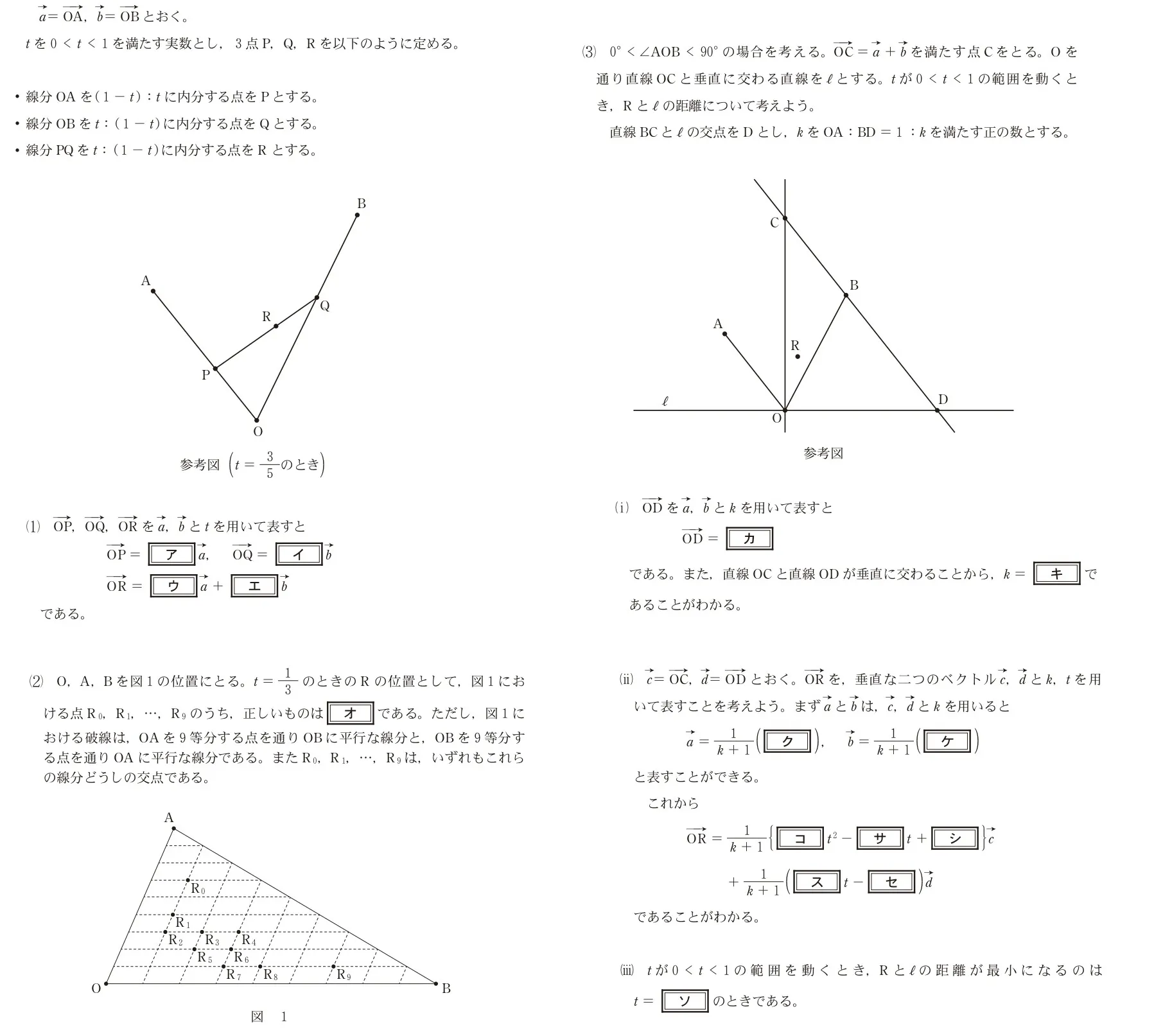
平面上に3点O、A、Bがある。ただし、O、A、Bは同一直線上にはないとする。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)追・試験 問110(数学Ⅱ・数学B(第5問) 問10) (訂正依頼・報告はこちら)
平面上に3点O、A、Bがある。ただし、O、A、Bは同一直線上にはないとする。

- 1/2
- 1/(k−1)
- 2/(k−1)
- 1/k
- 2/k
- (k−1)/k
- 1/(k+1)
- 2/(k+1)
- (k−1)/(k+1)
- k/(k+1)
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
PはOAを(1-t):tに内分する点だから
正解です。
lとの距離が最小になるには垂線すなわちベクトルCが重要であること、あとは正負の関係等を用いて最小限の計算で抑えることが出来たら最適です。
参考になった数0
この解説の修正を提案する
前の問題(問109)へ
令和6年度(2024年度)追・試験 問題一覧