大学入学共通テスト(数学) 過去問
令和7年度(2025年度)本試験
問49 (数学Ⅱ・数学B(第1問) 問2)
問題文
sin{θ+(π/6)}=sin2θ ・・・・・①
の解を求めよう。以下では、α=θ+(π/6)、β=2θとおく。
このとき、①は
sinα=sinβ ・・・・・②
となる。
(ⅰ)二つの一般角αとβが等しければ、sinαとsinβは等しい。
α=βを満たすθはπ/( ア )であり、これは①の解の一つである。
そして、θ=π/( ア )のとき
sin{θ+(π/6)}(=sin2θ=(√[ イ ])/( ウ )となる。
(ⅱ)太郎さんと花子さんは、θ=π/( ア )以外の①の解を求める方法について話している。
太郎:角が等しくなくても、サインの値が等しくなることがあるね。
花子:サインの値が等しくなるのはどんなときか、単位円を用いて考えてみようか。
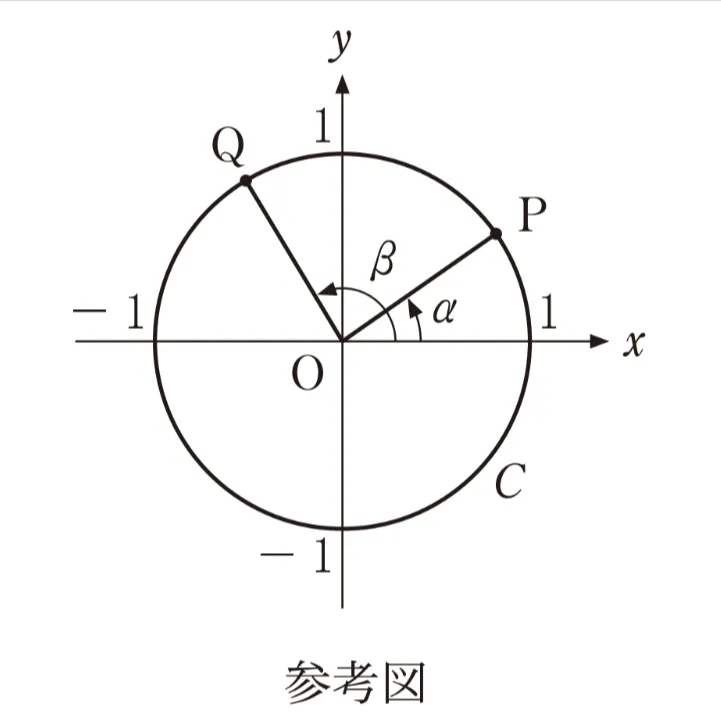
Oを原点とする座標平面において、中心がOで、半径が1の円をCとする。さらに、αの動径とCとの交点をP,βの動径とCとの交点をQとする。ここで、動径はOを中心とし、その始線はx軸の正の部分とする。
②が成り立つときに、点Pと点Qの間につねに成り立つ関係の記述として、正しいものは( エ )である。
(ⅲ)θ≠π/( ア )とする。
・0≦θ≦π/2の場合を考える。このとき、0≦β≦πであるので、②が成り立つとき、(ⅱ)で考察したことに注意すると、αとβは
α+β=( オ )
を満たすことがわかる。これより、0≦θ≦π/2のときの①の解
θ=([ カ ]/[ キク ])π
を得る。
・π/2<θ<πの場合を考える。
このとき、π<β<2πであるので、②が成り立つとき、(ⅱ)で考察したことに注意すると、αとβは
α+β=( ケ )
を満たすことがわかる。これより、π/2<θ<πのときの①の解
θ=([ コサ ]/[ シス ])π
を得る。
以上より、0≦θ<πのとき、①の解は
θ=π/( ア ),([ カ ]/[ キク ])π,([ コサ ]/[ シス ])π
である。
( イウ )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和7年度(2025年度)本試験 問49(数学Ⅱ・数学B(第1問) 問2) (訂正依頼・報告はこちら)
sin{θ+(π/6)}=sin2θ ・・・・・①
の解を求めよう。以下では、α=θ+(π/6)、β=2θとおく。
このとき、①は
sinα=sinβ ・・・・・②
となる。
(ⅰ)二つの一般角αとβが等しければ、sinαとsinβは等しい。
α=βを満たすθはπ/( ア )であり、これは①の解の一つである。
そして、θ=π/( ア )のとき
sin{θ+(π/6)}(=sin2θ=(√[ イ ])/( ウ )となる。
(ⅱ)太郎さんと花子さんは、θ=π/( ア )以外の①の解を求める方法について話している。
太郎:角が等しくなくても、サインの値が等しくなることがあるね。
花子:サインの値が等しくなるのはどんなときか、単位円を用いて考えてみようか。
Oを原点とする座標平面において、中心がOで、半径が1の円をCとする。さらに、αの動径とCとの交点をP,βの動径とCとの交点をQとする。ここで、動径はOを中心とし、その始線はx軸の正の部分とする。
②が成り立つときに、点Pと点Qの間につねに成り立つ関係の記述として、正しいものは( エ )である。
(ⅲ)θ≠π/( ア )とする。
・0≦θ≦π/2の場合を考える。このとき、0≦β≦πであるので、②が成り立つとき、(ⅱ)で考察したことに注意すると、αとβは
α+β=( オ )
を満たすことがわかる。これより、0≦θ≦π/2のときの①の解
θ=([ カ ]/[ キク ])π
を得る。
・π/2<θ<πの場合を考える。
このとき、π<β<2πであるので、②が成り立つとき、(ⅱ)で考察したことに注意すると、αとβは
α+β=( ケ )
を満たすことがわかる。これより、π/2<θ<πのときの①の解
θ=([ コサ ]/[ シス ])π
を得る。
以上より、0≦θ<πのとき、①の解は
θ=π/( ア ),([ カ ]/[ キク ])π,([ コサ ]/[ シス ])π
である。
( イウ )にあてはまるものを1つ選べ。

- イ:2 ウ:1
- イ:2 ウ:2
- イ:3 ウ:2
- イ:3 ウ:4
- イ:5 ウ:4
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問48)へ
令和7年度(2025年度)本試験 問題一覧
次の問題(問50)へ