大学入学共通テスト(数学) 過去問
令和7年度(2025年度)追・試験
問68 (数学Ⅱ・数学B(第4問) 問8)
問題文
c1=a,
cn+1=−1/2cn2+4(n=1,2,3,・・・)・・・・・①
花子さんと太郎さんは、数列{cn}について話している。
花子:一般項cnを求めてみようか。
太郎:一般項を式で表すのは難しそうだから、aとnをいろいろ変えてみて,cnの具体的な値を調べてみよう。
花子:コンピュータでたくさん計算してみたけれど、−4≦cn≦4が成り立つことが多いね。
太郎:−4≦ck≦4が成り立つと、−4≦ck+1≦4も成り立つように見えるね。
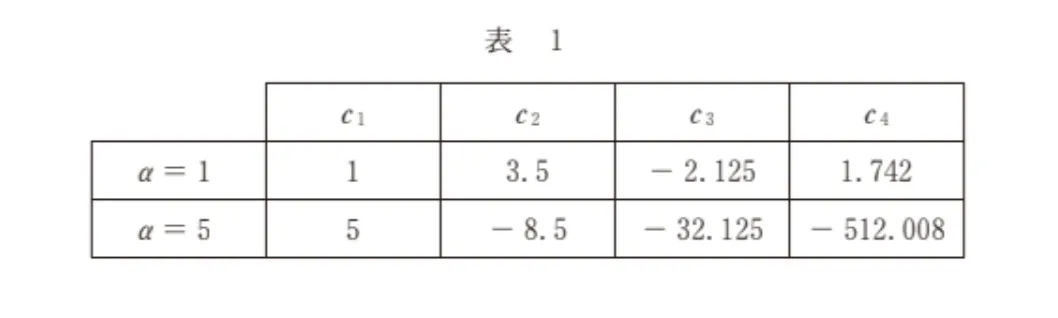
(ⅱ) 表1は、コンピュータによる計算結果の一部をまとめたものである。ただし、c4の値は小数第4位を四捨五入したものである。
aを変えて得られる数列{cn}に関する次の命題(Ⅰ),(Ⅱ),(Ⅲ)について、真偽の組合せとして正しいものは( ツ )である。
(Ⅰ) a>4ならば、すべての自然数nについてcn>4が成り立つ。
(Ⅱ) a≦4ならば、すべての自然数nについてcn≦4が成り立つ。
(Ⅲ) a<0ならば、すべての自然数nについてcn<0が成り立つ。
( ツ )にあてはまるものを一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和7年度(2025年度)追・試験 問68(数学Ⅱ・数学B(第4問) 問8) (訂正依頼・報告はこちら)
c1=a,
cn+1=−1/2cn2+4(n=1,2,3,・・・)・・・・・①
花子さんと太郎さんは、数列{cn}について話している。
花子:一般項cnを求めてみようか。
太郎:一般項を式で表すのは難しそうだから、aとnをいろいろ変えてみて,cnの具体的な値を調べてみよう。
花子:コンピュータでたくさん計算してみたけれど、−4≦cn≦4が成り立つことが多いね。
太郎:−4≦ck≦4が成り立つと、−4≦ck+1≦4も成り立つように見えるね。
(ⅱ) 表1は、コンピュータによる計算結果の一部をまとめたものである。ただし、c4の値は小数第4位を四捨五入したものである。
aを変えて得られる数列{cn}に関する次の命題(Ⅰ),(Ⅱ),(Ⅲ)について、真偽の組合せとして正しいものは( ツ )である。
(Ⅰ) a>4ならば、すべての自然数nについてcn>4が成り立つ。
(Ⅱ) a≦4ならば、すべての自然数nについてcn≦4が成り立つ。
(Ⅲ) a<0ならば、すべての自然数nについてcn<0が成り立つ。
( ツ )にあてはまるものを一つ選べ。

- (Ⅰ):真 (Ⅱ):真 (Ⅲ):真
- (Ⅰ):真 (Ⅱ):真 (Ⅲ):偽
- (Ⅰ):真 (Ⅱ):偽 (Ⅲ):真
- (Ⅰ):真 (Ⅱ):偽 (Ⅲ):偽
- (Ⅰ):偽 (Ⅱ):真 (Ⅲ):真
- (Ⅰ):偽 (Ⅱ):真 (Ⅲ):偽
- (Ⅰ):偽 (Ⅱ):偽 (Ⅲ):真
- (Ⅰ):偽 (Ⅱ):偽 (Ⅲ):偽
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
解答:(Ⅰ):偽、(Ⅱ):真、(Ⅲ):偽
解説:
命題(Ⅰ)について考えます。
α=5のとき、c2、c3、c4において負の値になっているので、偽です。
命題(Ⅱ)について考えます。
(タ)の結果より、すべてのkについて、ck≦4です。
よって、命題(Ⅱ)は真です。
命題(Ⅲ)について考えます。
α=-2のとき、①に代入すると、
c2=-1/2×(-2)2+4=0
よって、以上が反例なので、偽です。
参考になった数0
この解説の修正を提案する
前の問題(問67)へ
令和7年度(2025年度)追・試験 問題一覧
次の問題(問69)へ