大学入学共通テスト（数学） 過去問
令和4年度（2022年度）本試験
問71 (数学Ⅱ・数学B（第1問） 問15)
問題文
以下（ ツ ）に当てはまるものを選べ。
〔2〕a，bは正の実数であり、a≠1，b≠1を満たすとする。太郎さんは
logabとlogbaの大小関係を調べることにした。
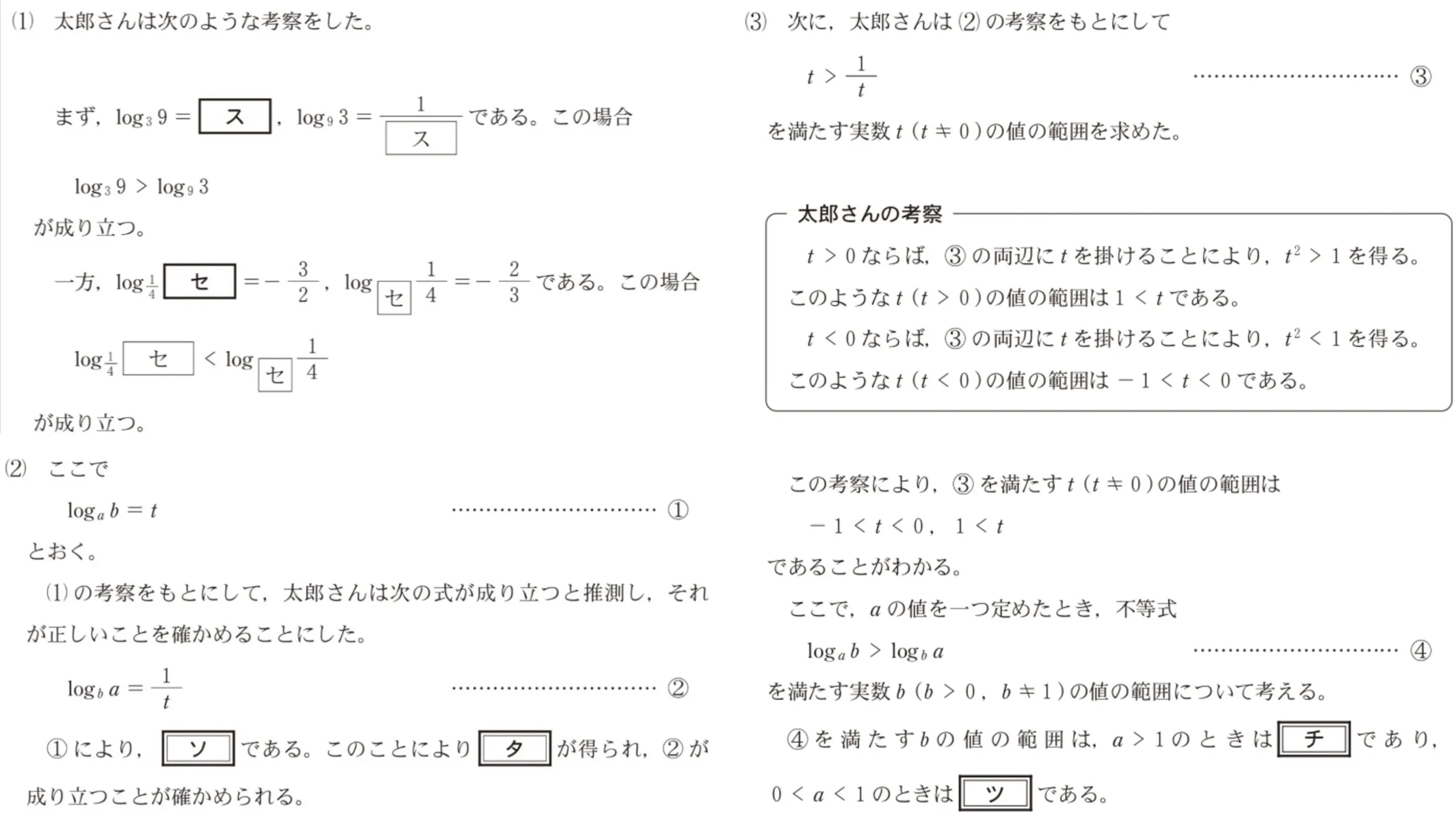
〔2〕a，bは正の実数であり、a≠1，b≠1を満たすとする。太郎さんは
logabとlogbaの大小関係を調べることにした。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和4年度（2022年度）本試験 問71（数学Ⅱ・数学B（第1問） 問15） （訂正依頼・報告はこちら）
以下（ ツ ）に当てはまるものを選べ。
〔2〕a，bは正の実数であり、a≠1，b≠1を満たすとする。太郎さんは
logabとlogbaの大小関係を調べることにした。
〔2〕a，bは正の実数であり、a≠1，b≠1を満たすとする。太郎さんは
logabとlogbaの大小関係を調べることにした。
- 0＜b＜a， 1＜b＜1／a
- 0＜b＜a， 1／a＜b
- a＜b＜1， 1＜b＜1／a
- a＜b＜1， 1／a＜b
正解！素晴らしいです
残念...
この過去問の解説 （2件）
01
丁寧な誘導がありますので、
それに乗って計算していきましょう。
logabは底aの値によって
大小関係が異なることに注意しましょう。
・1<aのとき
logabは、bが大きいほど大きくなる増加関数
・0<a<1のとき
logabは、bが大きいほど小さくなる減少関数
logab=tとおくと、
logab>logbaは、t>1/tと表せます。
これを満たすtの範囲は、
-1<t<0、1<tです。
・-1<logab<0については、
0<a<1ですから、1<b<a-1です。
・1<logabについては、
0<a<1ですから、b<aです。
また、真数条件より、b>0です。
以上まとめて、答えは0<b<a,1<b<1/aです。
参考になった数0
この解説の修正を提案する
02
対数に関する問題です。
自分のわかりやすい数字に置き換えて直感的な判断ができるようになると好ましいです。
問題文より、
ー1＜logab＜0、1＜logab
0＜a＜1のとき、
ー1＜logab＜0
1＜b＜1/a
1＜logab
0＜b＜aとなります。
参考になった数0
この解説の修正を提案する
前の問題（問70）へ
令和4年度（2022年度）本試験 問題一覧
次の問題（問72）へ