大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問87 (数学Ⅱ・数学B(第3問) 問3)
問題文
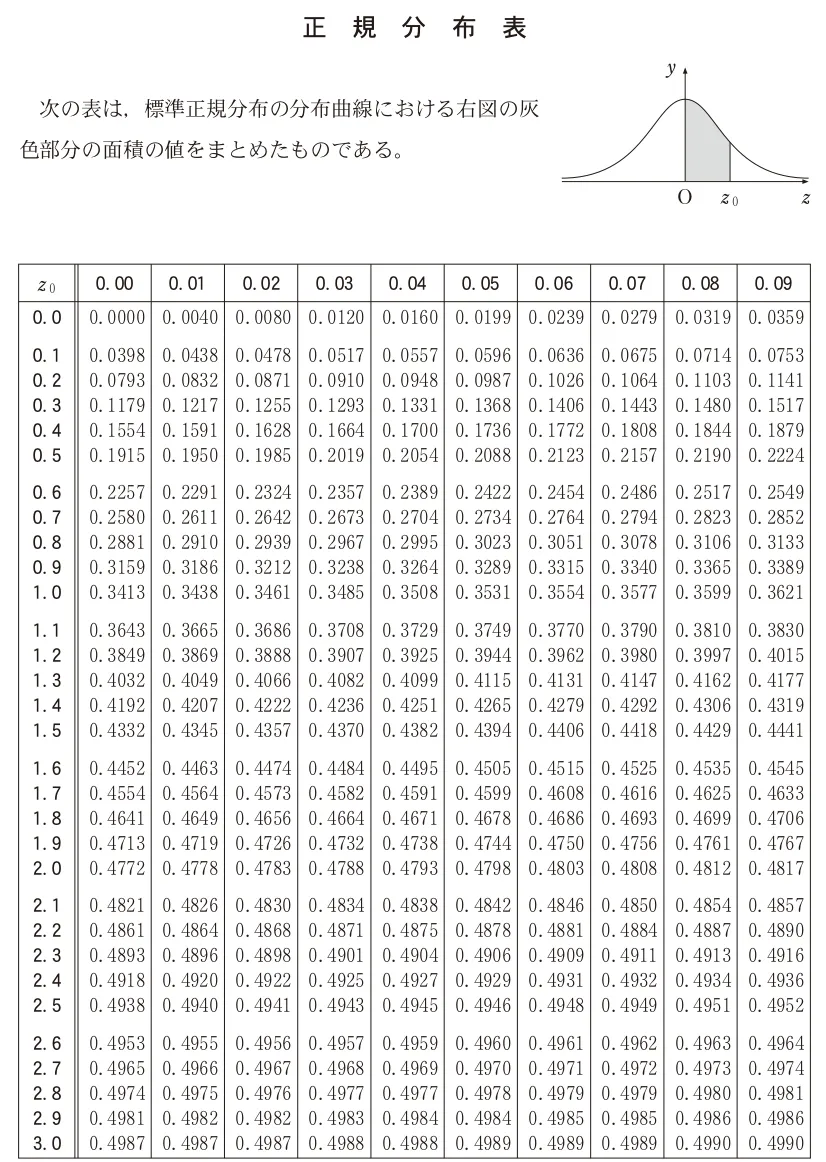
問題を解答するにあたっては、必要に応じて正規分布表を用いてもよい。
ジャガイモを栽培し販売している会社に勤務する花子さんは、A地区とB地区で収穫されるジャガイモについて調べることになった。
(1)A地区で収穫されるジャガイモには1個の重さが200gを超えるものが25%含まれることが経験的にわかっている。花子さんはA地区で収穫されたジャガイモから400個を無作為に抽出し、重さを計測した。そのうち、重さが200gを超えるジャガイモの個数を表す確率変数をZとする。このときZは二項分布B(400,0.[ アイ ])に従うから、Zの平均(期待値)は( ウエオ )である。
(2)Zを(1)の確率変数とし、A地区で収穫されたジャガイモ400個からなる標本において、重さが200gを超えていたジャガイモの標本における比率をR=Z/400とする。このとき、Rの標準偏差はσ(R)=( カ )である。
標本の大きさ400は十分に大きいので、Rは近似的に正規分布
N(0.[ アイ ],( カ )2)に従う。
したがって、P(R≧x)=0.0465となるようなxの値は( キ )となる。ただし、( キ )の計算においては√3=1.73とする。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)本試験 問87(数学Ⅱ・数学B(第3問) 問3) (訂正依頼・報告はこちら)
問題を解答するにあたっては、必要に応じて正規分布表を用いてもよい。
ジャガイモを栽培し販売している会社に勤務する花子さんは、A地区とB地区で収穫されるジャガイモについて調べることになった。
(1)A地区で収穫されるジャガイモには1個の重さが200gを超えるものが25%含まれることが経験的にわかっている。花子さんはA地区で収穫されたジャガイモから400個を無作為に抽出し、重さを計測した。そのうち、重さが200gを超えるジャガイモの個数を表す確率変数をZとする。このときZは二項分布B(400,0.[ アイ ])に従うから、Zの平均(期待値)は( ウエオ )である。
(2)Zを(1)の確率変数とし、A地区で収穫されたジャガイモ400個からなる標本において、重さが200gを超えていたジャガイモの標本における比率をR=Z/400とする。このとき、Rの標準偏差はσ(R)=( カ )である。
標本の大きさ400は十分に大きいので、Rは近似的に正規分布
N(0.[ アイ ],( カ )2)に従う。
したがって、P(R≧x)=0.0465となるようなxの値は( キ )となる。ただし、( キ )の計算においては√3=1.73とする。

- 3/6400
- √3/4
- √3/80
- 3/40
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
解答 カ: √3/80
解説
「Zの分散→Rの分散→Rの標準偏差」の順に考えていきましょう。
まず二項分布 B(n, p) に従う確率変数Zの分散は V(Z) = np(1-p) で求められます。
前問より、今考えている二項分布は B(400, 0.25) つまり n=400, p=0.25 ですから、
V(Z) = np(1-p) = 400×0.25×(1 - 0.25) = 75 となります。
確率変数aZ+bの分散はV(aZ+b) = a2V(Z)という性質があります。
よってRの分散は V(R) = V(Z/400) = V(Z)/4002 = 75/4002
です。
したがってRの標準偏差は
σ(R) = √V(R) = √(75/4002) = (5√3)/400 = √3/80
と求まり、答えは √3/80 となります。
補足
以下はアイの解説です(前問の解説から引用)。
この選択肢が答えとなります。
二項分布 B(n, p) に従う確率変数Zの分散は V(Z) = np(1-p) で求められます。
参考になった数1
この解説の修正を提案する
02
二項分布はB(n,p)と表されるので
B(400,0.25)
となります。
平均値はnpより
400×0.25=100
となります。
確率変数Zに従う比率R=Z/400の標準偏差は、
二項分布Bの標準偏差より
σ(R)
=√(400×0.25×(1-0.25))/400
=√(75)/400
=√3/80
となります。
正解です。
確率変数に従う、新たな確率変数における定義を再度復習しておくことが大切です。
参考になった数0
この解説の修正を提案する
前の問題(問86)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問88)へ