大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問104 (数学Ⅱ・数学B(第4問) 問11)
問題文
以下のように、歩行者と自転車が自宅を出発して移動と停止を繰り返している。歩行者と自転車の動きについて、数学的に考えてみよう。
自宅を原点とする数直線を考え、歩行者と自転車をその数直線上を動く点とみなす。数直線上の点の座標がyであるとき、その点は位置yにあるということにする。また、歩行者が自宅を出発してからx分経過した時点を時刻xと表す。歩行者は時刻0に自宅を出発し、正の向きに毎分1の速さで歩き始める。自転車は時刻2に自宅を出発し、毎分2の速さで歩行者を追いかける。自転車が歩行者に追いつくと、歩行者と自転車はともに1分だけ停止する。その後、歩行者は再び正の向きに毎分1の速さで歩き出し、自転車は毎分2の速さで自宅に戻る。自転車は自宅に到着すると、1分だけ停止した後、再び毎分2の速さで歩行者を追いかける。これを繰り返し、自転車は自宅と歩行者の間を往復する。
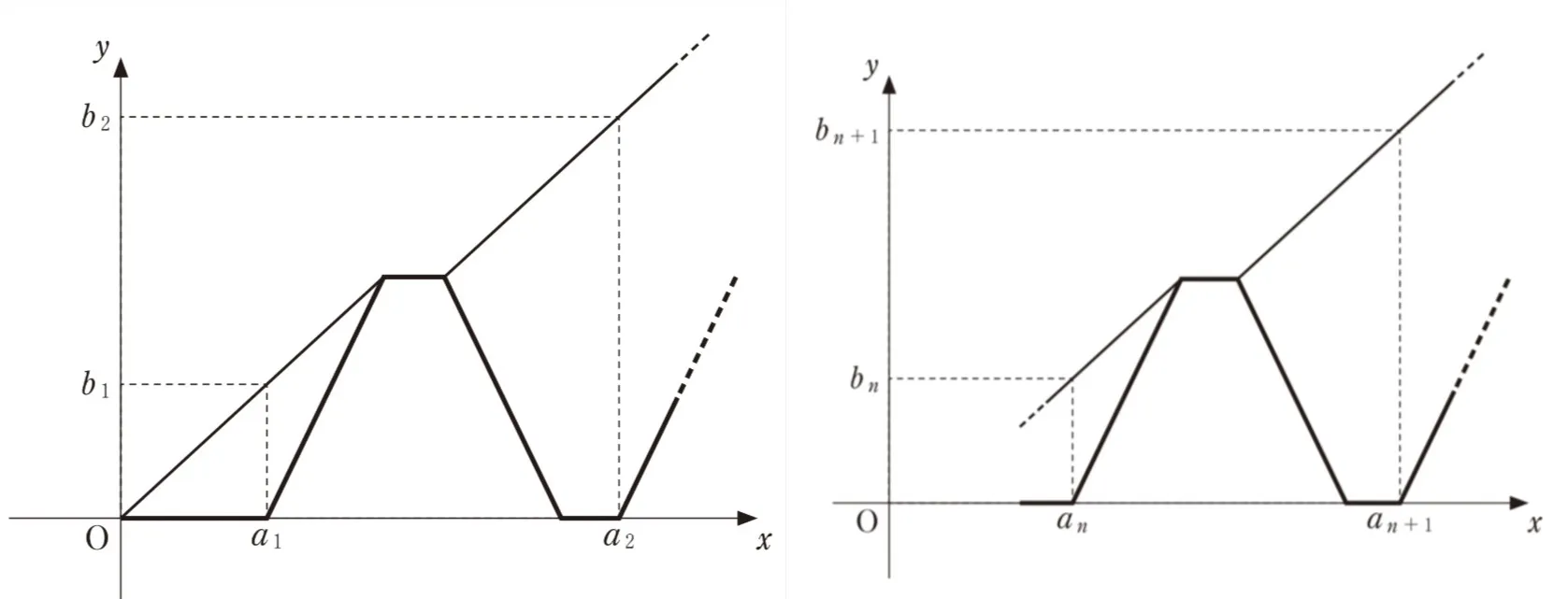
x=anを自転車がn回目に自宅を出発する時刻とし、y=bnをそのときの歩行者の位置とする。
(2)歩行者がy=300の位置に到着するときまでに、自転車が歩行者に追いつく回数は( サ )回である。また、( サ )回目に自転車が歩行者に追いつく時刻は、x=( シスセ )である。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)本試験 問104(数学Ⅱ・数学B(第4問) 問11) (訂正依頼・報告はこちら)
以下のように、歩行者と自転車が自宅を出発して移動と停止を繰り返している。歩行者と自転車の動きについて、数学的に考えてみよう。
自宅を原点とする数直線を考え、歩行者と自転車をその数直線上を動く点とみなす。数直線上の点の座標がyであるとき、その点は位置yにあるということにする。また、歩行者が自宅を出発してからx分経過した時点を時刻xと表す。歩行者は時刻0に自宅を出発し、正の向きに毎分1の速さで歩き始める。自転車は時刻2に自宅を出発し、毎分2の速さで歩行者を追いかける。自転車が歩行者に追いつくと、歩行者と自転車はともに1分だけ停止する。その後、歩行者は再び正の向きに毎分1の速さで歩き出し、自転車は毎分2の速さで自宅に戻る。自転車は自宅に到着すると、1分だけ停止した後、再び毎分2の速さで歩行者を追いかける。これを繰り返し、自転車は自宅と歩行者の間を往復する。
x=anを自転車がn回目に自宅を出発する時刻とし、y=bnをそのときの歩行者の位置とする。
(2)歩行者がy=300の位置に到着するときまでに、自転車が歩行者に追いつく回数は( サ )回である。また、( サ )回目に自転車が歩行者に追いつく時刻は、x=( シスセ )である。

- 125
- 127
- 135
- 137
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
解答 シスセ: 137
解説
この問題はエ・ケ・コ・サの答えを利用します。
n回目に自宅を出発した自転車が次に歩行者に追いつくときの時刻は、
エの答えより an+bn でした。
そして
ケの答えより bn = (5/2)・3n-1 -(1/2)
コの答えより an = (5/2)・3n-1 + n −(3/2)
であったので、
an+bn = 5・3n-1 + n - 2 です。
前問より サ: 4 だったので、x = a4+b4 を求めます。
x = a4+b4 = 5・33 + 4 - 2 = 5・27 + 1 = 135 + 2 = 137
よって答えは x=137 つまり シスセ: 137 となります。
補足
この問題はエ・ケ・コ・サの答えを利用します。
そのうちサの解説のみ以下に補足しておきます(前問より引用)。
サの解説
この選択肢が答えとなります。
参考になった数0
この解説の修正を提案する
02
これまでで求めた一般項を用います。
問い方が少し意地悪で引っ掛けが多いので気をつけましょう。
an=5/2・3n-1 +n-3/2
bn=2/5・3n-1-1/2を用います。
前問より、4回目に会う時の時間を求めます。
※前問では、n=5の場合を考えましたが、答えは4回なので、
今回考えるのはn=4の場合です。
n=4のとき、a4=5/2・33 +4-3/2=70
さらに、出会うまでにかかる時間が
b4=67ですので、
求める時間は70+67=137となります。
参考になった数0
この解説の修正を提案する
前の問題(問103)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問105)へ