大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問105 (数学Ⅱ・数学B(第5問) 問1)
問題文
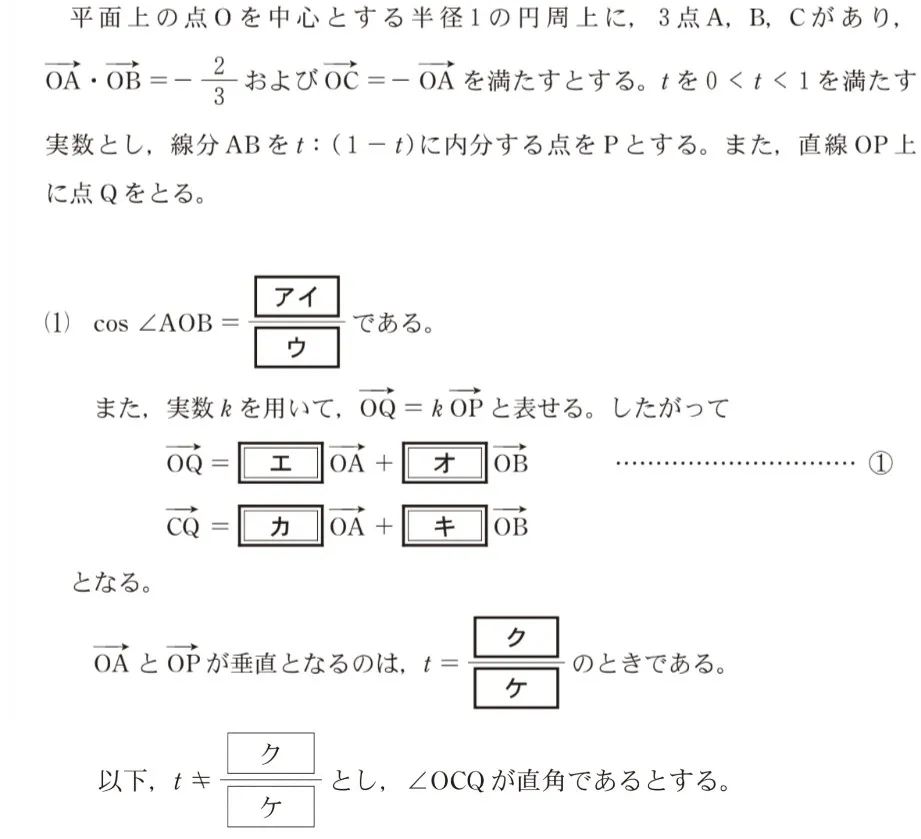
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)本試験 問105(数学Ⅱ・数学B(第5問) 問1) (訂正依頼・報告はこちら)

- アイ:−1 ウ:2
- アイ:−1 ウ:3
- アイ:−2 ウ:3
- アイ:−2 ウ:2
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
解答 ア: -(マイナス) イ: 2 ウ: 3 (アイ/ウ: -2/3)
解説
【表記に関する注意】
ここではベクトルを上に矢印をつけず右に添えて「OA→」などのように表記します。
まず (OA→)も (OB→) も大きさ1のベクトル(単位ベクトル)であり、つまり
|OA→|=|OB→|=1 であるので、
(OA→)・(OB→) = |OA→| |OB→| cos ∠AOB = cos ∠AOB …(式1)
となります。一方で問題文より、
(OA→)・(OB→) = -2/3 …(式2)
です。 (式1)と(式2)より、
答えは cos ∠AOB = -2/3 つまり アイ/ウ: -2/3 となります。
この選択肢が正解となります。
参考になった数0
この解説の修正を提案する
02
※この問題では「ベクトルa」を「→a」と表記します。
「→OA・→OB」は→OAと→OBの内積を表します。ここで内積の定義を確認しておきましょう。
→aと→bの内積を→a・→b、→aと→bのなす角をθとすると、
→a・→b=|→a||→b|cosθ
と表すことができます。
この問題では、cos∠AOBを求めます。
→OA・→OB=|→OA||→OB|cos∠AOB・・・・(*)
→OA・→OB、|→OA|、|→OB|の3つが分かれば、それらを(*)に代入すれば求めることができます。
まず問題文より→OA・→OB=-2/3です。OA、OBは円の半径なので、
|→OA|=|→OB|=1となります。
最後にこれらを(*)に代入すると、
-2/3=1×1×cos∠AOB
よって、cos∠AOB=-2/3となります。
cos∠AOB=-2/3(解説の冒頭にて解説)より
ア:−
イ:2
ウ:3
より誤
cos∠AOB=-2/3(解説の冒頭にて解説)より
ア:−
イ:2
ウ:3
より誤
cos∠AOB=-2/3(解説の冒頭にて解説)より
ア:−
イ:2
ウ:3
より正
cos∠AOB=-2/3(解説の冒頭にて解説)より
ア:−
イ:2
ウ:3
より誤
内積の定義
→a・→b=|→a||→b|cosθ
を覚えておくことがポイントです。
cosθなどが関わる問題は内積の定義を用いることが多いです。
参考になった数0
この解説の修正を提案する
前の問題(問104)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問106)へ