大学入学共通テスト(数学) 過去問
令和4年度(2022年度)追・再試験
問18 (数学Ⅰ・数学A(第2問) 問1)
問題文
aを5<a<10を満たす実数とする。長方形ABCDを考え、AB=CD=5、BC=DA=aとする。
次のようにして、長方形ABCDの辺上に4点P、Q、R、Sをとり、内部に点Tをとることを考える。
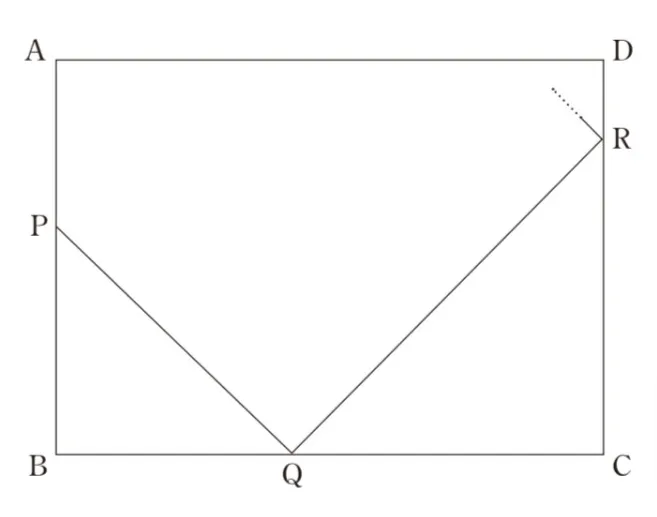
辺AB上に点Bと異なる点Pをとる。辺BC上に点Qを∠BPQが45°になるようにとる。Qを通り、直線PQと垂直に交わる直線をlとする。lが頂点C、D以外の点で辺CDと交わるとき、lと辺CDの交点をRとする。
点Rを通りlと垂直に交わる直線をmとする。mと辺ADとの交点をSとする。点Sを通りmと垂直に交わる直線をnとする。nと直線PQとの交点をTとする。
(1)a=6のとき、lが頂点C、D以外の点で辺CDと交わるときのAPの値の範囲は0≦AP<( ア )である。
このとき、四角形QRSTの面積の最大値は( イウ )/( エ )である。
a=8のとき、四角形QRSTの面積の最大値は( オカ )である。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)追・再試験 問18(数学Ⅰ・数学A(第2問) 問1) (訂正依頼・報告はこちら)
aを5<a<10を満たす実数とする。長方形ABCDを考え、AB=CD=5、BC=DA=aとする。
次のようにして、長方形ABCDの辺上に4点P、Q、R、Sをとり、内部に点Tをとることを考える。
辺AB上に点Bと異なる点Pをとる。辺BC上に点Qを∠BPQが45°になるようにとる。Qを通り、直線PQと垂直に交わる直線をlとする。lが頂点C、D以外の点で辺CDと交わるとき、lと辺CDの交点をRとする。
点Rを通りlと垂直に交わる直線をmとする。mと辺ADとの交点をSとする。点Sを通りmと垂直に交わる直線をnとする。nと直線PQとの交点をTとする。
(1)a=6のとき、lが頂点C、D以外の点で辺CDと交わるときのAPの値の範囲は0≦AP<( ア )である。
このとき、四角形QRSTの面積の最大値は( イウ )/( エ )である。
a=8のとき、四角形QRSTの面積の最大値は( オカ )である。

- 3
- 4
- 5
- 6
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
APの値(APの長さ)の範囲を求める問題なので、点Pが線分AB上でどのように動けるかを考えます。
最初、点Pが点Aと一致している時、すなわちAP=0のときは、4個の点P、Q、R、Sとそれらを結んだ直線は図1の水色の線となります。
ここで、点Pを点Bの方向にP→P’と移動した時は赤色の線で示されたものとなり、APの長さが大きくなるにつれ、点R’は次第に点Dに近づいていくことがわかります。そして、点Rと点Dが一致したときは、図2のようになります。
△BPQ、△CQRはともに直角二等辺三角形で、BP=BQ、CQ=CR であることから AP=4 が求まります。(図2 参照)
点Pがこの位置より下に移動した時(すなわち AP>4のとき)直線lは辺CDと交わらないので不適当。またAP=4 の時は点Rが点Dと一致することになり「直線lが頂点C、D以外の点で辺CDと交わる」という条件に反するので、AP≠4 です。
これより、点Pが直線AB上で動く範囲は図2の青い線で示した部分になり、APの値の範囲は、0≦AP<4 。
よって、解答欄(ア)には、数値「4」の選択番号が入ります。
どのように考えたらいいのか分かりにくい設問ですが、点Pの動きにつれて他の点がどのように動くかをみることによって、答えに近づくことができます。落ち着いて、しっかり考えてください。
参考になった数0
この解説の修正を提案する
02
まず図を書いて点Pを動かして実験していきましょう。
下の2つの図を見ると、Pを下に動かしていくにつれて、RがDに近づいていっているのがわかります。
(ア)ではRに近づける最大のAPの長さを求めれば良いです。つまり、RとDが一致するときのAPの長さを求めます。
AP=xとすると、
PB =5-x
PB=PQより、
BQ=5-x
BC=6より、
QC=BC-BQ=6-(5-x)=1+x
QC=CRより、
CR=1+x
CD=5より
RD=5-(1+x)=4-x
ここでRとDが一致するとき、RD=0より、
4-x=0
つまり、
x=4
となります。
よって、0≦AP<4が求める条件です。
0≦AP<4より誤りです。
0≦AP<4より正解です。
0≦AP<4より誤りです。
0≦AP<4より誤りです。
このような図形の問題は点を積極的にうごかして実験する事がとても重要です。
この問題では、点Pを下に下げすぎると、点RがいつかADに到達してしまう事に気づく必要がありました。
参考になった数0
この解説の修正を提案する
前の問題(問17)へ
令和4年度(2022年度)追・再試験 問題一覧
次の問題(問19)へ