大学入学共通テスト(数学) 過去問
令和4年度(2022年度)追・再試験
問19 (数学Ⅰ・数学A(第2問) 問2)
問題文
aを5<a<10を満たす実数とする。長方形ABCDを考え、AB=CD=5、BC=DA=aとする。
次のようにして、長方形ABCDの辺上に4点P、Q、R、Sをとり、内部に点Tをとることを考える。
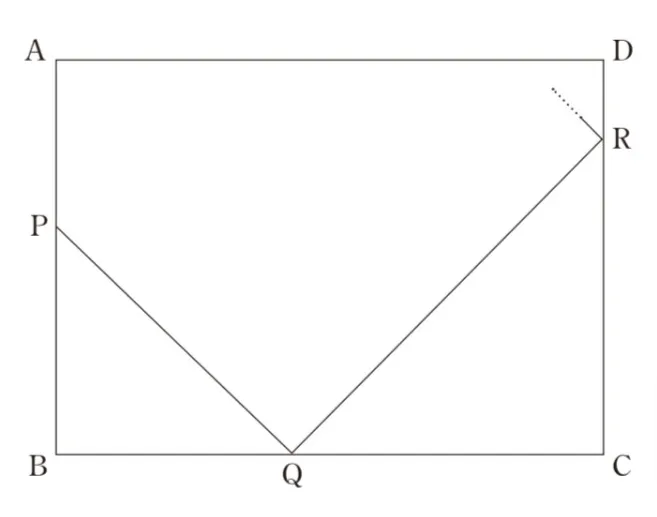
辺AB上に点Bと異なる点Pをとる。辺BC上に点Qを∠BPQが45°になるようにとる。Qを通り、直線PQと垂直に交わる直線をlとする。lが頂点C、D以外の点で辺CDと交わるとき、lと辺CDの交点をRとする。
点Rを通りlと垂直に交わる直線をmとする。mと辺ADとの交点をSとする。点Sを通りmと垂直に交わる直線をnとする。nと直線PQとの交点をTとする。
(1)a=6のとき、lが頂点C、D以外の点で辺CDと交わるときのAPの値の範囲は0≦AP<( ア )である。
このとき、四角形QRSTの面積の最大値は( イウ )/( エ )である。
a=8のとき、四角形QRSTの面積の最大値は( オカ )である。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)追・再試験 問19(数学Ⅰ・数学A(第2問) 問2) (訂正依頼・報告はこちら)
aを5<a<10を満たす実数とする。長方形ABCDを考え、AB=CD=5、BC=DA=aとする。
次のようにして、長方形ABCDの辺上に4点P、Q、R、Sをとり、内部に点Tをとることを考える。
辺AB上に点Bと異なる点Pをとる。辺BC上に点Qを∠BPQが45°になるようにとる。Qを通り、直線PQと垂直に交わる直線をlとする。lが頂点C、D以外の点で辺CDと交わるとき、lと辺CDの交点をRとする。
点Rを通りlと垂直に交わる直線をmとする。mと辺ADとの交点をSとする。点Sを通りmと垂直に交わる直線をnとする。nと直線PQとの交点をTとする。
(1)a=6のとき、lが頂点C、D以外の点で辺CDと交わるときのAPの値の範囲は0≦AP<( ア )である。
このとき、四角形QRSTの面積の最大値は( イウ )/( エ )である。
a=8のとき、四角形QRSTの面積の最大値は( オカ )である。

- イウ:25 エ:2
- イウ:26 エ:5
- イウ:27 エ:4
- イウ:29 エ:6
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
AP=xとおいて、四角形QRSTの面積をxで表します。
まず、△BPQ、△CQRはともに直角二等辺三角形で、
BP=BQ、CQ=CR
かつ PQ=√2BQ、QR=√2CQ ・・(a)
AP=x とおくと 前問(ア)の結果より 0≦x<4 で、
BP=BQ=5–x
CQ=CB–QB=6–(5–x)=x+1
よって、CQ=CR=x+1
DR=DC–CR=5–(x+1)=–x+4
また(a)により、QR=√2CQ=√2(x+1)、
RS=√2DR=√2(–x+4)
よって、四角形QRSTの面積をS(x)とおくと、
S(x)=QR×RS
=√2(x+1)・√2(–x+4)
=2(–x2+3x+4)
=–2(x2–3x–4)
S(x)はxの2次関数となるので、平方完成してグラフをかき、最大値を求めます。
S(x)=–2(x2–3x–4)
=–2(x2–3x)+8
=–2{(x–3/2)2–9/4}+8
=–2(x–3/2)2+25/2
0≦x<4 より、S(x)はx=3/2のとき、最大値25/2をとります。
よって、解答欄(イウ)が「25」、(エ)が「2」となる選択肢の番号が入ります。
AP=xとおくと、四角形QRSTの面積はxの2次関数となります。そのあとは、2次関数の平方完成→グラフから最大値を読み取る、という超頻出のパターンとなり、比較的容易に解を求めることができます。
参考になった数0
この解説の修正を提案する
02
AP=xとして辺の長さを求めると、
PB =5-x
PB=PQより、
BQ=5-x
BC=6より、
QC=BC-BQ=6-(5-x)=1+x
QC=CRより、
CR=1+x
CD=5より
RD=5-(1+x)=4-x
となります。
ここで四角形の面積をもとめます。三平方の定理(1:1:√2)より
QR=√2QC, RS=√2RD
を用います。
四角形の面積をSとおくと、
S=QR×RS=√2QC×√2RD=2QC×RD=2(1+x)(4-x)=-2(x+1)(x-4)=-2(x2-3x-4)
これを平方完成すると、
-2{ (x-3/2)2-(25/4) }=-2(x-3/2)2+(25/2)
となり、
x=3/2のとき、最大値25/2を取ります。
0≦AP(=x)<4より、この値は有効です。
25/2より正解です。
25/2より誤りです。
25/2より誤りです。
25/2より誤りです。
動く辺の長さAPをひとつxとすると、残りの辺の長さはすべてxでかけます。
このおかげで面積が2次関数で表す事ができるので、最大値を求める事ができます。
また、二次関数の最大・最小値を求める時は平方完成を行うことも忘れないようにしましょう。
参考になった数0
この解説の修正を提案する
前の問題(問18)へ
令和4年度(2022年度)追・再試験 問題一覧
次の問題(問20)へ