大学入学共通テスト(数学) 過去問
令和4年度(2022年度)追・再試験
問24 (数学Ⅰ・数学A(第2問) 問7)
問題文
国土交通省では「全国道路・街路交通情勢調査」を行い、地域ごとのデータを公開している。以下では、2010年と2015年に67地域で調査された高速道路の交通量と速度を使用する。交通量としては、それぞれの地域において、ある1日にある区間を走行した自動車の台数(以下、交通量という。単位は台)を用いる。また、速度としては、それぞれの地域において、ある区間を走行した自動車の走行距離および走行時間から算出した値(以下、速度という。単位はkm/h)を用いる。
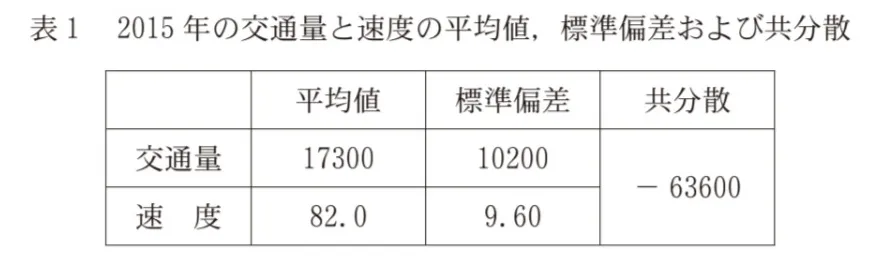
(1)表1は、2015年の交通量と速度の平均値、標準偏差および共分散である。ただし、共分散は交通量の偏差と速度の偏差の積の平均値である。
この表より、(標準偏差):(平均値)の比の値は、小数第3位を四捨五入すると、交通量については0.59であり、速度については( テ )である。また、交通量と速度の相関係数は( ト )である。
また、図1は、2015年の交通量と速度の散布図である。なお、この散布図には、完全に重なっている点はない。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)追・再試験 問24(数学Ⅰ・数学A(第2問) 問7) (訂正依頼・報告はこちら)
国土交通省では「全国道路・街路交通情勢調査」を行い、地域ごとのデータを公開している。以下では、2010年と2015年に67地域で調査された高速道路の交通量と速度を使用する。交通量としては、それぞれの地域において、ある1日にある区間を走行した自動車の台数(以下、交通量という。単位は台)を用いる。また、速度としては、それぞれの地域において、ある区間を走行した自動車の走行距離および走行時間から算出した値(以下、速度という。単位はkm/h)を用いる。
(1)表1は、2015年の交通量と速度の平均値、標準偏差および共分散である。ただし、共分散は交通量の偏差と速度の偏差の積の平均値である。
この表より、(標準偏差):(平均値)の比の値は、小数第3位を四捨五入すると、交通量については0.59であり、速度については( テ )である。また、交通量と速度の相関係数は( ト )である。
また、図1は、2015年の交通量と速度の散布図である。なお、この散布図には、完全に重なっている点はない。

- −0.71
- −0.65
- −0.59
- −0.12
- −0.03
- 0.03
- 0.12
- 0.59
- 0.65
- 0.71
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
(標準偏差):(平均値)の比の値を求めよ、という問題の指示に従っていきます。
速度について、標準偏差 9.60 を平均値 82.0 で割ると
9.60/82.0 ≒ 0.1170 となります。
少数第3位を四捨五入して、0.12。
よって、解答欄(テ)には「0.12」の選択肢の番号が入ります。
与えられた値を割り算すればOKです。計算ミスなど、厳禁です。
ちなみにですが、(標準偏差):(平均値)の比の値を変動係数といいます。(教科書には載っていないので、覚える必要はありません。)
参考になった数0
この解説の修正を提案する
02
比の値を計算する問題です。
(標準偏差)/(平均値)を計算すれば良いです。
9.6/82=0.117≒0.12
となります。
0.12より不適です。
0.12より不適です。
0.12より不適です。
0.12より不適です。
0.12より不適です。
0.12より不適です。
0.12より正解です。
0.12より不適です。
0.12より不適です。
0.12より不適です。
どっちでどっちを割るのかを間違えないようにしましょう。交通量のほうで例が示されているので、それに従って計算をしましょう。
参考になった数0
この解説の修正を提案する
前の問題(問23)へ
令和4年度(2022年度)追・再試験 問題一覧
次の問題(問25)へ