大学入学共通テスト（数学） 過去問
令和4年度（2022年度）追・再試験
問32 (数学Ⅰ・数学A（第2問） 問15)
問題文
以下（ ヘ ）に当てはまるものを選べ。
国土交通省では「全国道路・街路交通情勢調査」を行い、地域ごとのデータを公開している。以下では、2010年と2015年に67地域で調査された高速道路の交通量と速度を使用する。交通量としては、それぞれの地域において、ある1日にある区間を走行した自動車の台数（以下、交通量という。単位は台）を用いる。また、速度としては、それぞれの地域において、ある区間を走行した自動車の走行距離および走行時間から算出した値（以下、速度という。単位はkm／h）を用いる。
（3）図3は2015年の速度の箱ひげ図である。図4は2015年の交通量と速度の散布図である。これらの速度から1kmあたりの走行時間（分）を考える。例えば、速度が55km／hの場合は、1時間あたりの走行距離が55kmなので、1kmあたりの走行時間は（1／55）✕60の小数第位を四捨五入して1.09分となる。
このようにして2015年の速度を1kmあたりの走行時間に変換したデータの箱ひげ図は（ ヘ ）であり、2015年の交通量と1kmあたりの走行時間の散布図は（ ホ ）である。なお、解答群の散布図には、完全に重なっている点はない。
国土交通省では「全国道路・街路交通情勢調査」を行い、地域ごとのデータを公開している。以下では、2010年と2015年に67地域で調査された高速道路の交通量と速度を使用する。交通量としては、それぞれの地域において、ある1日にある区間を走行した自動車の台数（以下、交通量という。単位は台）を用いる。また、速度としては、それぞれの地域において、ある区間を走行した自動車の走行距離および走行時間から算出した値（以下、速度という。単位はkm／h）を用いる。
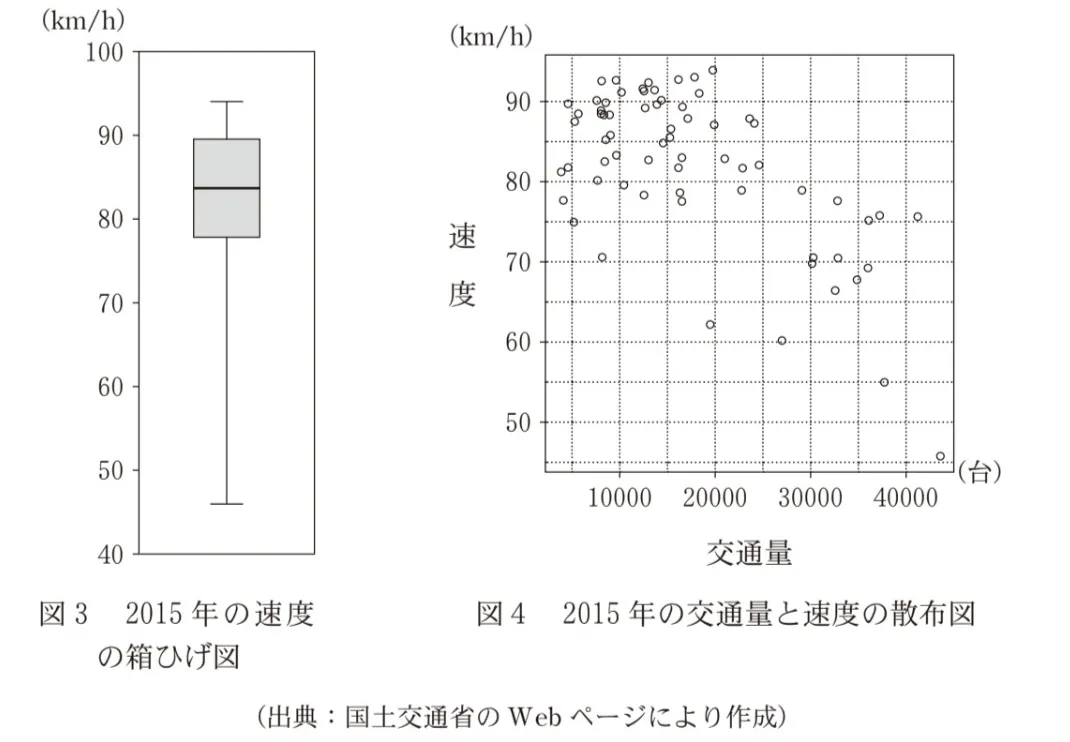
（3）図3は2015年の速度の箱ひげ図である。図4は2015年の交通量と速度の散布図である。これらの速度から1kmあたりの走行時間（分）を考える。例えば、速度が55km／hの場合は、1時間あたりの走行距離が55kmなので、1kmあたりの走行時間は（1／55）✕60の小数第位を四捨五入して1.09分となる。
このようにして2015年の速度を1kmあたりの走行時間に変換したデータの箱ひげ図は（ ヘ ）であり、2015年の交通量と1kmあたりの走行時間の散布図は（ ホ ）である。なお、解答群の散布図には、完全に重なっている点はない。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和4年度（2022年度）追・再試験 問32（数学Ⅰ・数学A（第2問） 問15） （訂正依頼・報告はこちら）
以下（ ヘ ）に当てはまるものを選べ。
国土交通省では「全国道路・街路交通情勢調査」を行い、地域ごとのデータを公開している。以下では、2010年と2015年に67地域で調査された高速道路の交通量と速度を使用する。交通量としては、それぞれの地域において、ある1日にある区間を走行した自動車の台数（以下、交通量という。単位は台）を用いる。また、速度としては、それぞれの地域において、ある区間を走行した自動車の走行距離および走行時間から算出した値（以下、速度という。単位はkm／h）を用いる。
（3）図3は2015年の速度の箱ひげ図である。図4は2015年の交通量と速度の散布図である。これらの速度から1kmあたりの走行時間（分）を考える。例えば、速度が55km／hの場合は、1時間あたりの走行距離が55kmなので、1kmあたりの走行時間は（1／55）✕60の小数第位を四捨五入して1.09分となる。
このようにして2015年の速度を1kmあたりの走行時間に変換したデータの箱ひげ図は（ ヘ ）であり、2015年の交通量と1kmあたりの走行時間の散布図は（ ホ ）である。なお、解答群の散布図には、完全に重なっている点はない。
国土交通省では「全国道路・街路交通情勢調査」を行い、地域ごとのデータを公開している。以下では、2010年と2015年に67地域で調査された高速道路の交通量と速度を使用する。交通量としては、それぞれの地域において、ある1日にある区間を走行した自動車の台数（以下、交通量という。単位は台）を用いる。また、速度としては、それぞれの地域において、ある区間を走行した自動車の走行距離および走行時間から算出した値（以下、速度という。単位はkm／h）を用いる。
（3）図3は2015年の速度の箱ひげ図である。図4は2015年の交通量と速度の散布図である。これらの速度から1kmあたりの走行時間（分）を考える。例えば、速度が55km／hの場合は、1時間あたりの走行距離が55kmなので、1kmあたりの走行時間は（1／55）✕60の小数第位を四捨五入して1.09分となる。
このようにして2015年の速度を1kmあたりの走行時間に変換したデータの箱ひげ図は（ ヘ ）であり、2015年の交通量と1kmあたりの走行時間の散布図は（ ホ ）である。なお、解答群の散布図には、完全に重なっている点はない。
正解！素晴らしいです
残念...
この過去問の解説 （2件）
01
例えば、速さが２倍になれば１ｋｍの移動に要する走行時間は半分になる事からも分かるように、１ｋｍあたりの走行(移動)時間は速度に反比例します。これより、いずれも１ｋｍあたりの走行(移動)時間を考えて、
速度が最小 → 走行時間は最大
速度の第１四分位数 → 走行時間の第３四分位数
速度の第２四分位数(中間値) → 走行時間の第２四分位数(中間値)
速度の第３四分位数 → 走行時間の第１四分位数
速度が最大 → 走行時間は最小
という関係が成り立ちます。
これをもとに、４つの選択肢の箱ひげ図が正しいかどうかをみていきますが、その前に図３から速度を読み取り、１ｋｍあたりの走行時間に変換しておきます。
図３から、速度の最大値、最小値、第２四分位数はそれぞれおよそ９４ｋｍ、４５ｋｍ、８４ｋｍで、その時の走行時間はそれぞれ
(１／９４)☓６０＝０.６４(分) (走行時間の最小値)
(１／４５)☓６０＝１.３３(分) (走行時間の最大値)
(１／８４)☓６０＝０.７１(分) (走行時間の第２四分位数)
となります。
ここで４つの選択肢(箱ひげ図)を見ると第２四分位数の値がすべて異なっており、第２四分位数が０.７１になっているかどうかで確認していきます。
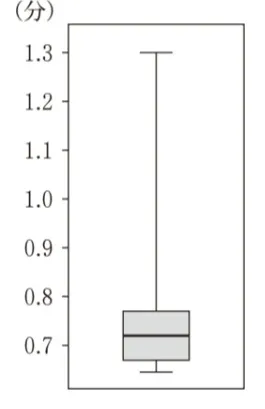
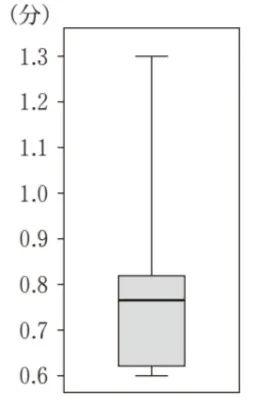
第２四分位数を見ると間違いとはいえません。
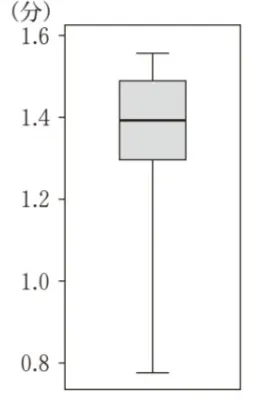
第２四分位数が１.４に近い値になっていて、正しい箱ひげ図とはいえません。
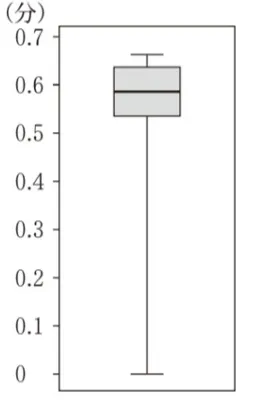
第２四分位数が０.６より少し小さい値になっていて、正しい箱ひげ図とはいえません。
第２四分位数が０.７７あたりの値になっていて、正しい箱ひげ図とはいえません。
問２７と同じように、間違いがあるものを除外していく、という考え方ですが、この問題の場合は選択肢にある箱ひげ図の第２四分位数がすべて異なる値なので、第２四分位数の値で調べる方が効率的です。いくつかある選択肢の中の値が異なっているところを見つけ、その値で正誤を判断するとわかりやすいと思います。
参考になった数0
この解説の修正を提案する
02
箱ひげ図を選ぶ問題では特徴的な量に着目しましょう。
この場合は、中央値の値に着目します。箱ひげ図での中央値は箱の中にある黒い線で表されます。
図3では、2015年の速度の中央値は約84です。この数字を元に、1kmあたりの走行時間に変換すると、
(1/84)×60=0.714...≒0.71となります。
選択肢の箱ひげ図で中央値がこれに近いものは一つしかありません。
中央値は0.71になるので、正解です。
中央値は0.71になるので、誤りです。
中央値は0.71になるので、誤りです。
中央値は0.71になるので、誤りです。
今回は中央値に着目しましたが、最大値・最小値・第1四分位数・第3四分位数に着目する問題もたくさんありますので、注意するようにしましょう。
参考になった数0
この解説の修正を提案する
前の問題（問31）へ
令和4年度（2022年度）追・再試験 問題一覧
次の問題（問33）へ