大学入学共通テスト(数学) 過去問
令和4年度(2022年度)追・再試験
問114 (数学Ⅱ・数学B(第4問) 問10)
問題文
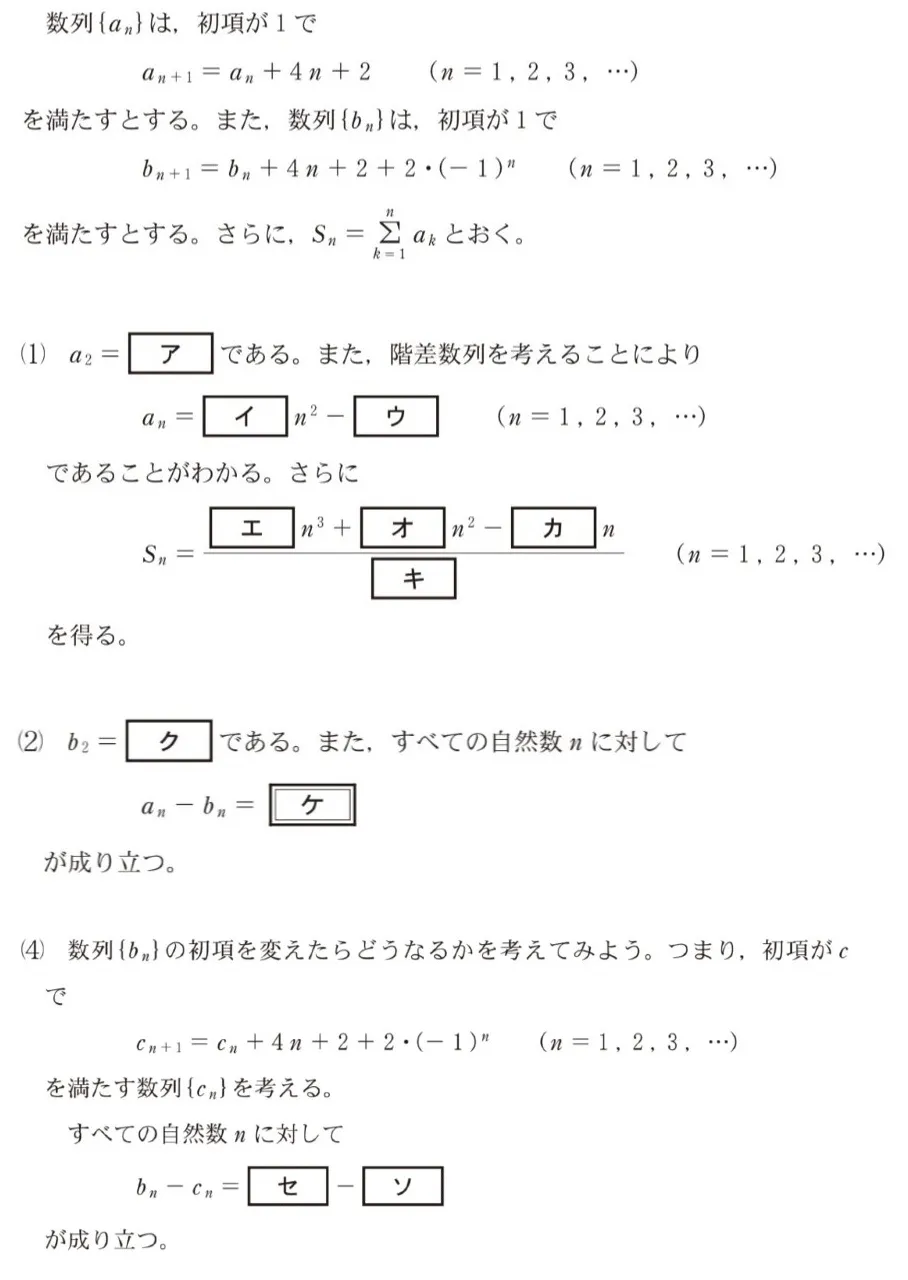
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)追・再試験 問114(数学Ⅱ・数学B(第4問) 問10) (訂正依頼・報告はこちら)

- セ:1 ソ:c
- セ:2 ソ:c
- セ:1 ソ:1
- セ:2 ソ:1
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
(2)と同様に
数列{bn}と数列{cn}の辺々を引くと
bn+1=bn+4n+2+2・(-1)n
-) cn+1=cn+4n+2+2・(-1)n
bn+1-cn+1=bn-cn ・・・①
となります。
bn-cn=ynとおくと、
①は
yn+1=yn
と表すことができます。
つまり数列{yn}は、
すべての項が同じ値の数列です。
b1=1,c1=cなので
y1=1-c
であるが、
数列{yn}はすべての項が同じ値なので
yn=1-c
よって、
bn-cn=1-c
正解です。
不正解です。
不正解です。
不正解です。
参考になった数0
この解説の修正を提案する
02
ここで、b1=1、c1=cより
bn-cn=1-cとなります。
bn-cn=1-cとなるため、正解です。
bn-cn=1-cとなるため、不正解です。
bn-cn=1-cとなるため、不正解です。
bn-cn=1-cとなるため、不正解です。
(2)と同様に数列同士を引き算していくことがpointです。
参考になった数0
この解説の修正を提案する
前の問題(問113)へ
令和4年度(2022年度)追・再試験 問題一覧
次の問題(問115)へ