大学入学共通テスト(数学) 過去問
令和4年度(2022年度)追・再試験
問127 (数学Ⅱ・数学B(第5問) 問10)
問題文
aを正の実数とする。Oを原点とする座標空間に4点
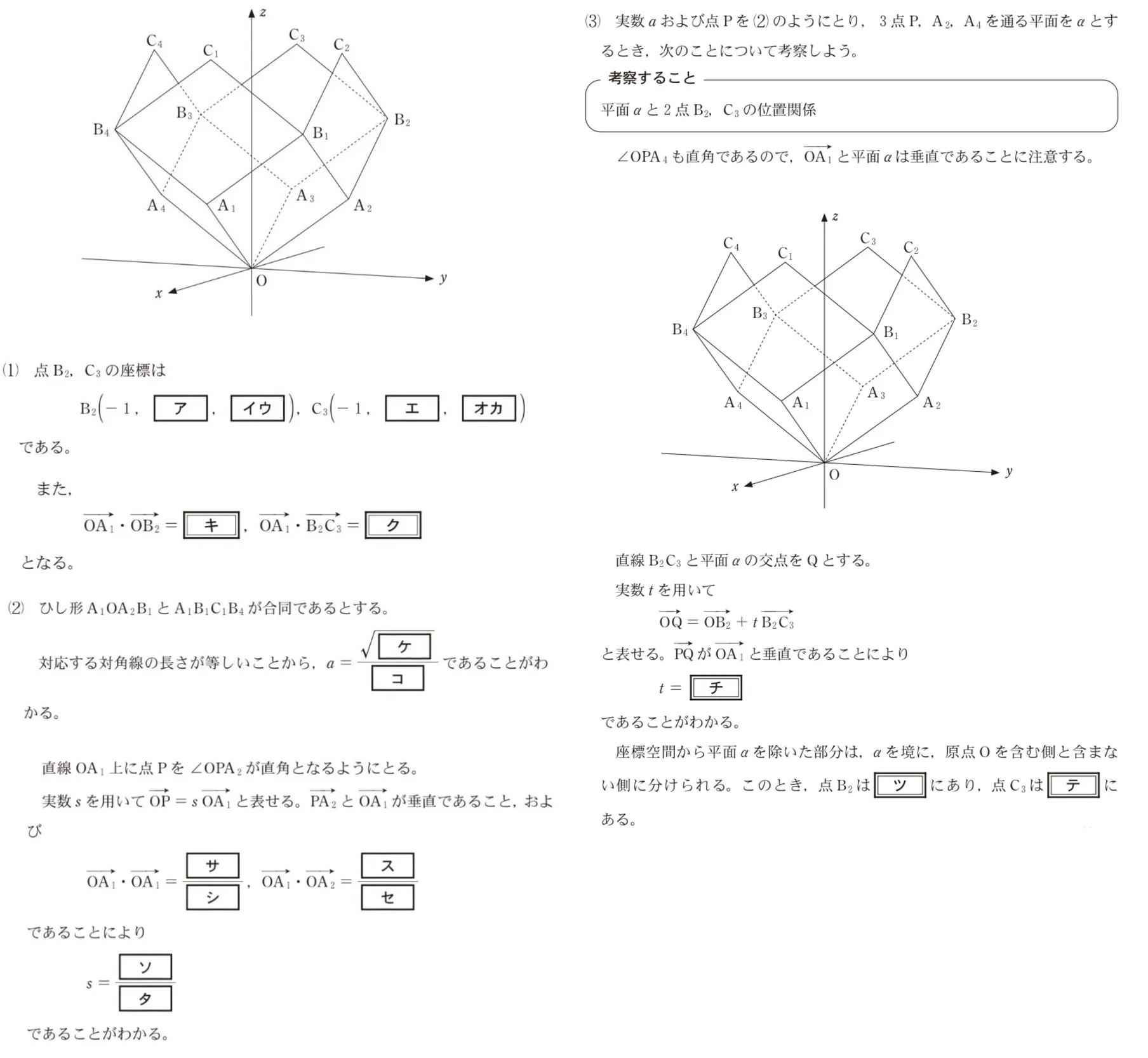
A1(1,0,a)、A2(0,1,a)、A3(−1,0,a)、A4(0,−1,a)がある。また、次の図のように、4点B1、B2、B3、B4を四角形A1OA2B1、A2OA3B2、A3OA4B3、A4OA1B4がそれぞれひし形になるようにとる。さらに、4点C1、C2、C3、C4を四角形A1B1C1B4、A2B2C2B1、A3B3C3B2、A4B4C4B3がそれぞれひし形になるようにとる。
ただし、座標空間における四角形を考える際には、その四つの頂点が同一平面上にあるものとする。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)追・再試験 問127(数学Ⅱ・数学B(第5問) 問10) (訂正依頼・報告はこちら)
aを正の実数とする。Oを原点とする座標空間に4点
A1(1,0,a)、A2(0,1,a)、A3(−1,0,a)、A4(0,−1,a)がある。また、次の図のように、4点B1、B2、B3、B4を四角形A1OA2B1、A2OA3B2、A3OA4B3、A4OA1B4がそれぞれひし形になるようにとる。さらに、4点C1、C2、C3、C4を四角形A1B1C1B4、A2B2C2B1、A3B3C3B2、A4B4C4B3がそれぞれひし形になるようにとる。
ただし、座標空間における四角形を考える際には、その四つの頂点が同一平面上にあるものとする。

- a上
- Oを含む側
- Oを含まない側
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
t=1より
OQ→=OB2→+B2C3→
=OC3→
となるので点Qと点C3は一致します。
つまり、点C3は平面α上にあります。
また、
OA1→・OB2→=2(√2/2)2-1=0
なのでOB2→はOA1→と垂直です。
このことからαとOB2→は
平行であることがわかります。
よって点B2は平面αに対して
原点Oと同じ側にあります。
不正解です。
正解です。
不正解です。
参考になった数0
この解説の修正を提案する
02
ベクトルB2C3=ベクトルOA4
だから、B2は原点に対応することが分かります。
したがって原点側です。
Oを含む側であるため、不正解です。
Oを含む側であるため、正解です。
Oを含む側であるため、不正解です。
算出したQを示すことで位置関係が把握できます。
参考になった数0
この解説の修正を提案する
前の問題(問126)へ
令和4年度(2022年度)追・再試験 問題一覧
次の問題(問128)へ