大学入学共通テスト(数学) 過去問
令和5年度(2023年度)本試験
問16 (数学Ⅰ・数学A(第2問) 問3)
問題文
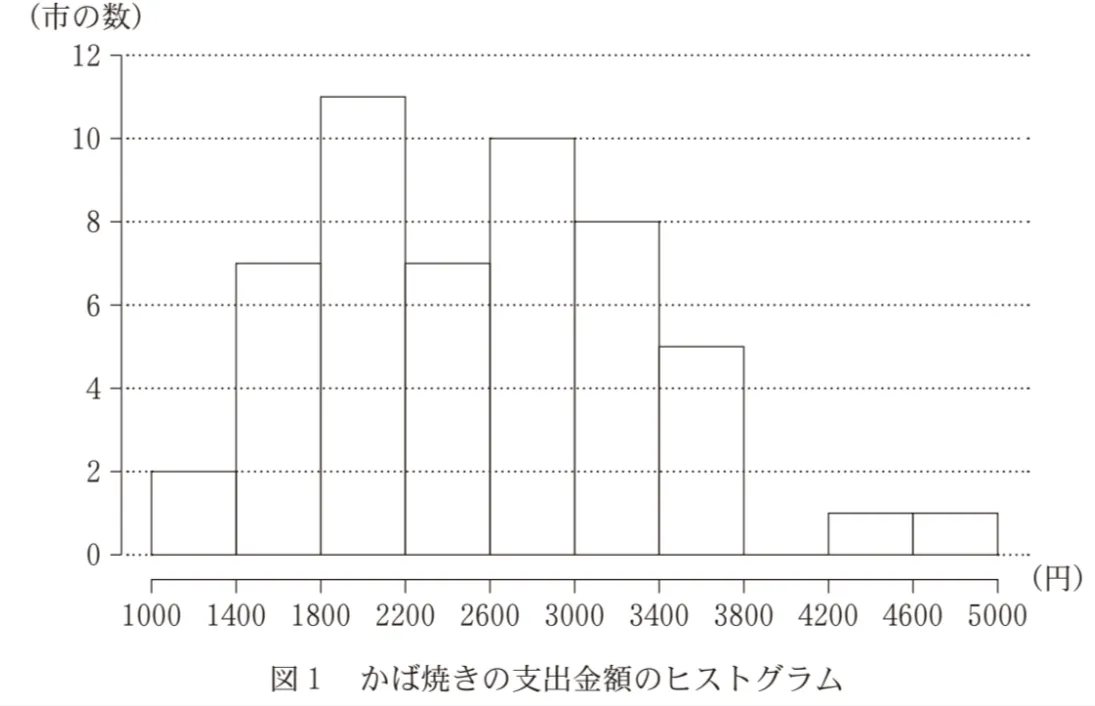
太郎さんは調理食品として、最初にうなぎのかば焼き(以下、かば焼き)に着目し、図1のように52市におけるかば焼きの支出金額のヒストグラムを作成した。ただし、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
なお、以下の図や表については、総務省のWebページをもとに作成している。
(1)図1から次のことが読み取れる。
・第1四分位数が含まれる階級は( ア )である。
・第3四分位数が含まれる階級は( イ )である。
・四分位範囲は( ウ )。
( ウ )にあてはまるものを次のうちから1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)本試験 問16(数学Ⅰ・数学A(第2問) 問3) (訂正依頼・報告はこちら)
太郎さんは調理食品として、最初にうなぎのかば焼き(以下、かば焼き)に着目し、図1のように52市におけるかば焼きの支出金額のヒストグラムを作成した。ただし、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
なお、以下の図や表については、総務省のWebページをもとに作成している。
(1)図1から次のことが読み取れる。
・第1四分位数が含まれる階級は( ア )である。
・第3四分位数が含まれる階級は( イ )である。
・四分位範囲は( ウ )。
( ウ )にあてはまるものを次のうちから1つ選べ。

- 800より小さい
- 800より大きく1600より小さい
- 1600より大きく2400より小さい
- 2400より大きく3200より小さい
- 3200より大きく4000より小さい
- 4000より大きい
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
四分位範囲=第3四分位数-第1四分位数
です。
問14 と問15 の解説で第1四分位数,第3四分位数が
含まれる階級をそれぞれ求めています。
(問14 の解説より)
(問15 の解説より)
以上のことから,第1四分位数Q1,第3四分位数Q3について
1800≦Q1<2200 かつ 3000≦Q3<3400
であることがわかります。よって,
Q3―Q1≧3000-Q1>3000-2200
すなわち Q3―Q1≧800……①
また,
Q3―Q1<3400-Q1≦3400-1800
すなわち Q3―Q1<1600……②
が成り立つので,①,②より
800<Q3―Q1<1600
すなわち,四分位範囲は 800 より大きく 1600 より小さい
正解です。
「四分位範囲」の意味を正しく理解していれば,
あまり難易度の高い問題ではありません。
「四分位偏差」という用語もあり,
こちらは四分位範囲を 2 で割った値です。
用語の理解に不安がある人は,
まず教科書に太字で出てくる用語の意味を
しっかり理解しましょう。
参考になった数0
この解説の修正を提案する
02
第1四分位数と第3四分位数、四分位範囲の定義から該当する値を読み取る問題です。
今、データ総数が52個で、第1四分位数は13番目と14番目のデータの平均値、第3四分位数は39番目と40番目のデータの平均値、四分位範囲はこの差を考えれば良いです。
小さい順に、2,7,11,7,10,8,5,0,1,1のデータが各階級に含まれていることから
四分位範囲は3000-2200=800, 3400-1800=1600より、800より大きく、1600より小さい。
参考になった数0
この解説の修正を提案する
前の問題(問15)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問17)へ