大学入学共通テスト(数学) 過去問
令和5年度(2023年度)本試験
問17 (数学Ⅰ・数学A(第2問) 問4)
問題文
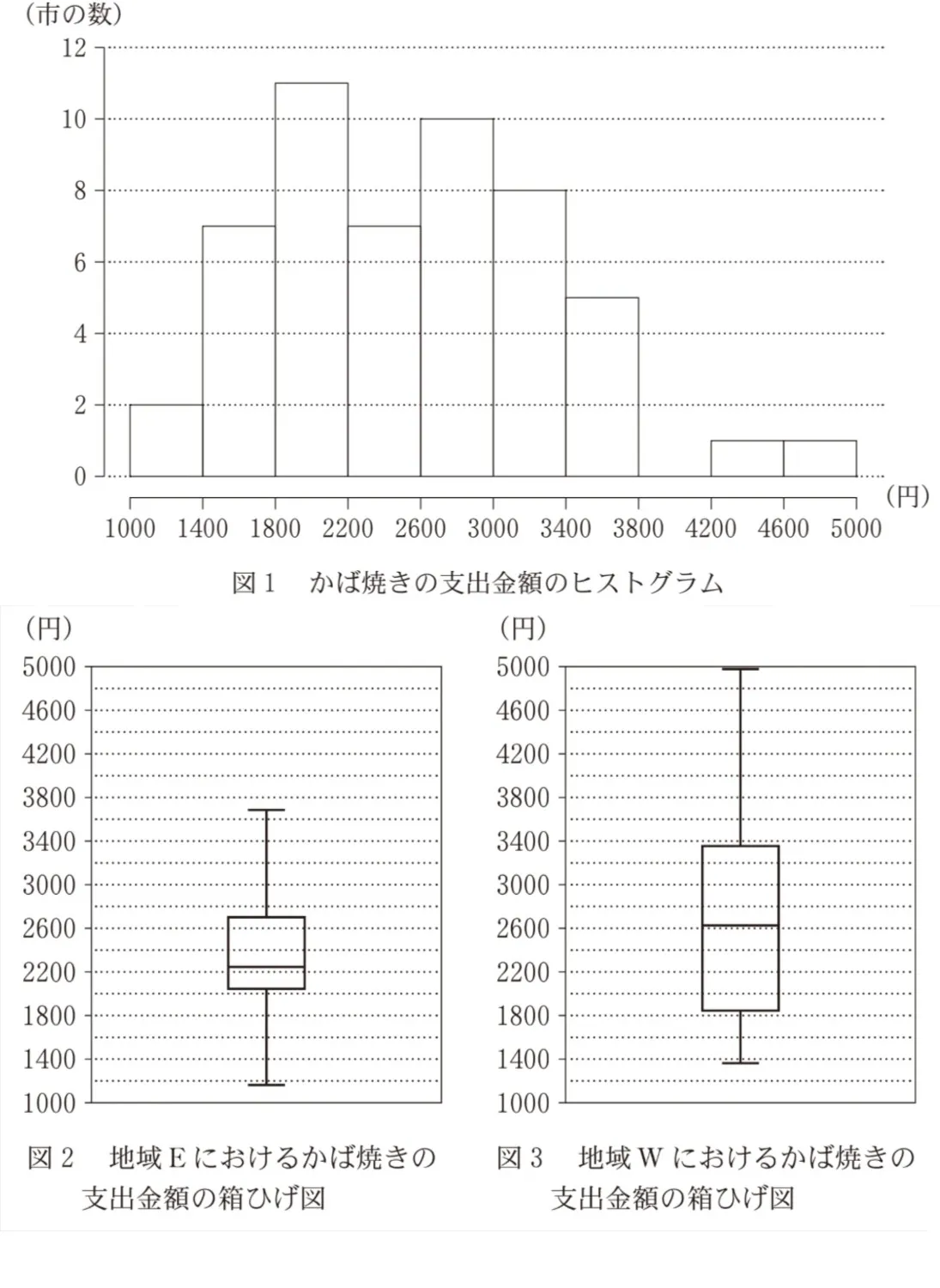
太郎さんは調理食品として、最初にうなぎのかば焼き(以下、かば焼き)に着目し、図1のように52市におけるかば焼きの支出金額のヒストグラムを作成した。ただし、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
なお、以下の図や表については、総務省のWebページをもとに作成している。
(2)太郎さんは、東西での地域による食文化の違いを調べるために、52市を東側の地域E(19市)と西側の地域W(33市)の二つに分けて考えることにした。
(ⅰ)地域Eと地域Wについて、かば焼きの支出金額の箱ひげ図を、図2、図3のようにそれぞれ作成した。
かば焼きの支出金額について、図2と図3から読み取れることとして、次のうち、正しいものは( エ )である。
( エ )にあてはまるものを次のうちから1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)本試験 問17(数学Ⅰ・数学A(第2問) 問4) (訂正依頼・報告はこちら)
太郎さんは調理食品として、最初にうなぎのかば焼き(以下、かば焼き)に着目し、図1のように52市におけるかば焼きの支出金額のヒストグラムを作成した。ただし、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
なお、以下の図や表については、総務省のWebページをもとに作成している。
(2)太郎さんは、東西での地域による食文化の違いを調べるために、52市を東側の地域E(19市)と西側の地域W(33市)の二つに分けて考えることにした。
(ⅰ)地域Eと地域Wについて、かば焼きの支出金額の箱ひげ図を、図2、図3のようにそれぞれ作成した。
かば焼きの支出金額について、図2と図3から読み取れることとして、次のうち、正しいものは( エ )である。
( エ )にあてはまるものを次のうちから1つ選べ。

-
地域Eにおいて、小さい方から5番目は2000以下である。
- 地域Eと地域Wの範囲は等しい。
- 中央値は、地域Eより地域Wの方が大きい。
- 2600未満の市の割合は、地域Eより地域Wの方が大きい。
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
箱ひげ図は,下の図のように最大値・最小値と四分位数を視覚的に表現する図です。
また,
範囲=最大値-最小値,
四分位範囲=第3四分位数-第1四分位数
ですから,範囲と四分位範囲も,
箱ひげ図から読み取ることができます。
地域Eにおいて、小さい方から5番目は2000以下である。
誤りです。
地域Eは19市ですから,中央値(第2四分位数)は
金額の小さい方から10番目の数値となります。
よって第1四分位数は,小さい方から
1番目,2番目,……,9番目
の中央値,すなわち小さい方から5番目です。
つまり,問題で問われている「小さい方から5番目」とは,
第1四分位数のことです。
箱ひげ図を見ると,地域Eの第1四分位数は,
2000の目盛り(1800と2200の間の線)よりも
上にあることがわかります。
したがって,この選択肢は誤りです。
誤りです。
箱ひげ図を見比べると,明らかに
地域Wの範囲の方が地域Eの範囲よりも
大きいことがわかります。
したがって,この選択肢は誤りです。
正解です。
箱ひげ図を見比べると,
地域Eの中央値は2600より小さく,
地域Wの中央値は2600以上です。
したがって,この選択肢は正解です。
誤りです。
地域Eでは中央値の市も含めて過半数の市が2600未満で
あるため,その割合は50%より大きくなります。
一方地域Wは33市なので,小さい方から17番目の数値が
中央値となります。
この中央値の市も含めて過半数の市が2600以上で
あるため,2600未満の市は半数未満です。
すなわち,地域Wは2600未満の市の割合は50%未満です。
したがって,この選択肢は誤りです。
箱ひげ図の問題では,四分位数がどのように定義されているかを
しっかり理解した上で考えていきましょう。
参考になった数0
この解説の修正を提案する
前の問題(問16)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問18)へ