大学入学共通テスト(数学) 過去問
令和5年度(2023年度)本試験
問19 (数学Ⅰ・数学A(第2問) 問6)
問題文
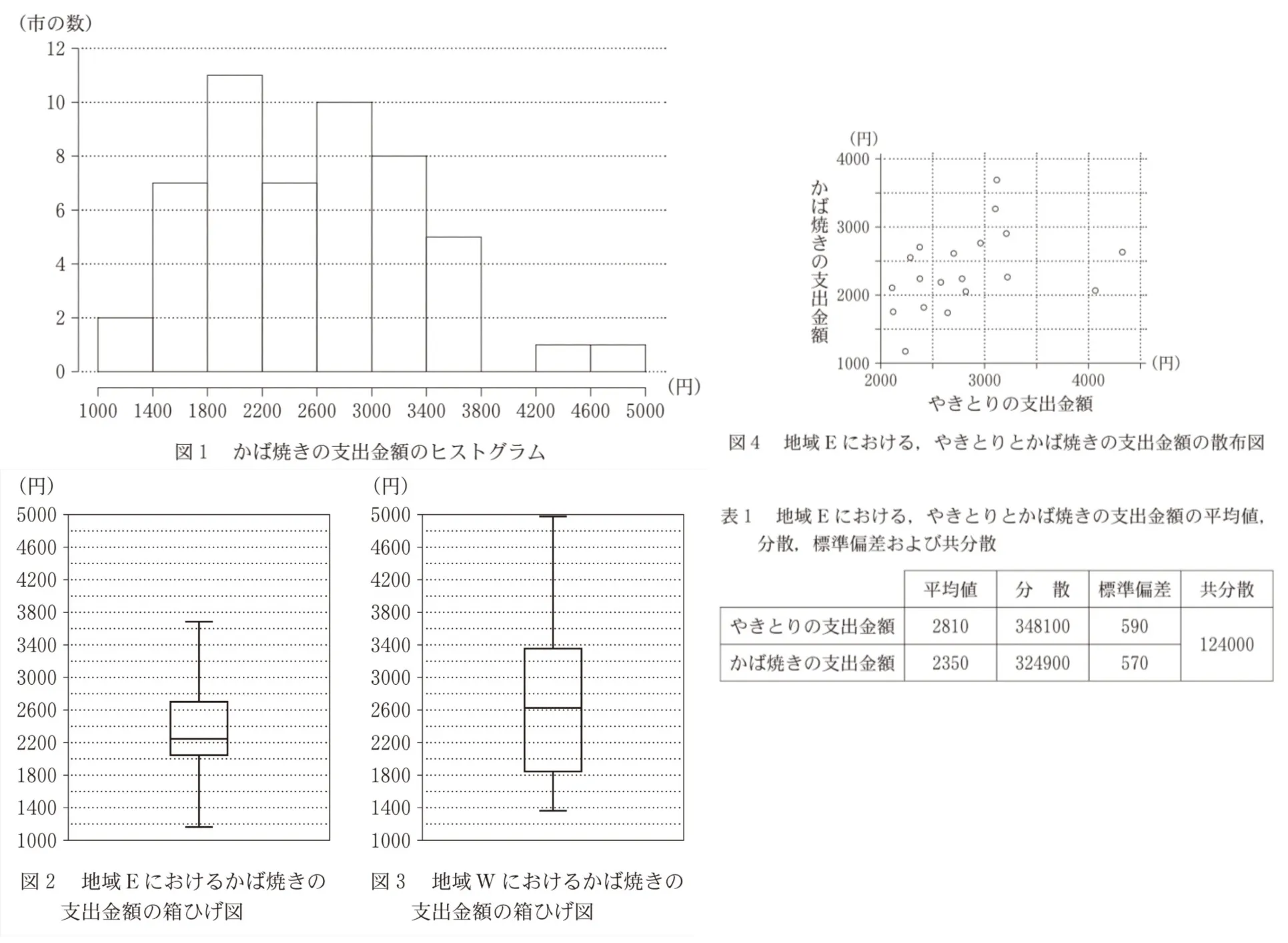
太郎さんは調理食品として、最初にうなぎのかば焼き(以下、かば焼き)に着目し、図1のように52市におけるかば焼きの支出金額のヒストグラムを作成した。ただし、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
なお、以下の図や表については、総務省のWebページをもとに作成している。
(2)太郎さんは、東西での地域による食文化の違いを調べるために、52市を東側の地域E(19市)と西側の地域W(33市)の二つに分けて考えることにした。
(ⅰ)地域Eと地域Wについて、かば焼きの支出金額の箱ひげ図を、図2、図3のようにそれぞれ作成した。
かば焼きの支出金額について、図2と図3から読み取れることとして、次のうち、正しいものは( エ )である。
(ⅱ)太郎さんは、地域Eと地域Wのデータの散らばりの度合いを数値でとらえようと思い、それぞれの分散を考えることにした。地域Eにおけるかば焼きの支出金額の分散は、地域Eのそれぞれの市におけるかば焼きの支出金額の偏差の( オ )である。
(3)太郎さんは、(2)で考えた地域Eにおける、やきとりの支出金額についても調べることにした。
ここでは地域Eにおいて、やきとりの支出金額が増加すれば、かば焼きの支出金額も増加する傾向があるのではないかと考え、まず図4のように、地域Eにおける、やきとりとかば焼きの支出金額の散布図を作成した。そして、相関係数を計算するために、表1のように平均値、分散、標準偏差および共分散を算出した。ただし、共分散は地域Eのそれぞれの市における、やきとりの支出金額の偏差とかば焼きの支出金額の偏差との積の平均値である。
表1を用いると、地域Eにおける、やきとりの支出金額とかば焼きの支出金額の相関係数は( カ )である。
( カ )については、最も適当なものを、次のうちから一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)本試験 問19(数学Ⅰ・数学A(第2問) 問6) (訂正依頼・報告はこちら)
太郎さんは調理食品として、最初にうなぎのかば焼き(以下、かば焼き)に着目し、図1のように52市におけるかば焼きの支出金額のヒストグラムを作成した。ただし、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
なお、以下の図や表については、総務省のWebページをもとに作成している。
(2)太郎さんは、東西での地域による食文化の違いを調べるために、52市を東側の地域E(19市)と西側の地域W(33市)の二つに分けて考えることにした。
(ⅰ)地域Eと地域Wについて、かば焼きの支出金額の箱ひげ図を、図2、図3のようにそれぞれ作成した。
かば焼きの支出金額について、図2と図3から読み取れることとして、次のうち、正しいものは( エ )である。
(ⅱ)太郎さんは、地域Eと地域Wのデータの散らばりの度合いを数値でとらえようと思い、それぞれの分散を考えることにした。地域Eにおけるかば焼きの支出金額の分散は、地域Eのそれぞれの市におけるかば焼きの支出金額の偏差の( オ )である。
(3)太郎さんは、(2)で考えた地域Eにおける、やきとりの支出金額についても調べることにした。
ここでは地域Eにおいて、やきとりの支出金額が増加すれば、かば焼きの支出金額も増加する傾向があるのではないかと考え、まず図4のように、地域Eにおける、やきとりとかば焼きの支出金額の散布図を作成した。そして、相関係数を計算するために、表1のように平均値、分散、標準偏差および共分散を算出した。ただし、共分散は地域Eのそれぞれの市における、やきとりの支出金額の偏差とかば焼きの支出金額の偏差との積の平均値である。
表1を用いると、地域Eにおける、やきとりの支出金額とかば焼きの支出金額の相関係数は( カ )である。
( カ )については、最も適当なものを、次のうちから一つ選べ。

- −0.62
- −0.50
- −0.37
- −0.19
- −0.02
- 0.02
- 0.19
- 0.37
- 0.50
- 0.62
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
相関係数は,次の公式で求めることができます。
求める相関係数は,
124000÷(590×570)=0.368…
となり,選択肢の中でこれに最も近い値は 0.37 です。
正解です。
相関係数を求める問題ですが,標準偏差と共分散が与えられているので,
公式さえ知っていれば,あてはめて計算するだけです。
計算ミスのないように気をつけましょう。
相関係数等については,データが一部訂正されたり追加されたりしたときに
分散,標準偏差,相関係数などがどのように変化するか
(大きくなる,小さくなる,変わらない等)を問う問題が
出題された年度もあります。
他の年度の問題もしっかり研究しておきましょう。
参考になった数0
この解説の修正を提案する
02
相関係数の計算をする問題。共分散が表で与えられているため、公式を覚えていればさほど難しくはないでしょう。
データxとyの相関係数は
(xとyの共分散)/(xの標準偏差)×(yの標準偏差)
で与えられるので、表の値を用いて
124999/(590×570) ≅ 0.37
参考になった数0
この解説の修正を提案する
前の問題(問18)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問20)へ