大学入学共通テスト（数学） 過去問
令和5年度（2023年度）本試験
問22 (数学Ⅰ・数学A（第2問） 問9)
問題文
（ サ ）にあてはまるものを次のうちから1つ選べ。
〔2〕太郎さんと花子さんは、バスケットボールのプロ選手の中には、リングと同じ高さでシュートを打てる人がいることを知り、シュートを打つ高さによってボールの軌道がどう変わるかについて考えている。
二人は、図1のように座標軸が定められた平面上に、プロ選手と花子さんがシュートを打つ様子を真横から見た図をかき、ボールがリングに入った場合について、後の仮定を設定して考えることにした。長さの単位はメートルであるが、以下では省略する。
＜仮定＞
・平面上では、ボールを直径0.2の円とする。
・リングを真横から見たときの左端を点A（3.8，3）、右端を点B（4.2，3）とし、リングの太さは無視する。
・ボールがリングや他のものに当たらずに上からリングを通り、かつ、ボールの中心がABの中点M（4，3）を通る場合を考える。ただし、ボールがリングに当たるとは、ボールの中心とAまたはBとの距離が0.1以下になることとする。
・プロ選手がシュートを打つ場合のボールの中心を点Pとし、Pは、はじめに点P0（0，3）にあるものとする。また、P0，Mを通る、上に凸の放物線をC1とし、PはC1上を動くものとする。
・花子さんがシュートを打つ場合のボールの中心を点Hとし、Hは、はじめに点H0（0，2）にあるものとする。また、H0，Mを通る、上に凸の放物線をC2とし、HはC2上を動くものとする。
・放物線C1やC2に対して、頂点のy座標を「シュートの高さ」とし、頂点のx座標を「ボールが最も高くなるときの地上の位置」とする。
（1）放物線C1の方程式におけるx2の係数をaとする。放物線C1の方程式は
y＝ax2−（ キ ）ax＋（ ク ）
と表すことができる。また、プロ選手の「シュートの高さ」は
—（ ケ ）a＋（ コ ）
である。
プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」の比較の記述として、正しいものは（ サ ）である。
〔2〕太郎さんと花子さんは、バスケットボールのプロ選手の中には、リングと同じ高さでシュートを打てる人がいることを知り、シュートを打つ高さによってボールの軌道がどう変わるかについて考えている。
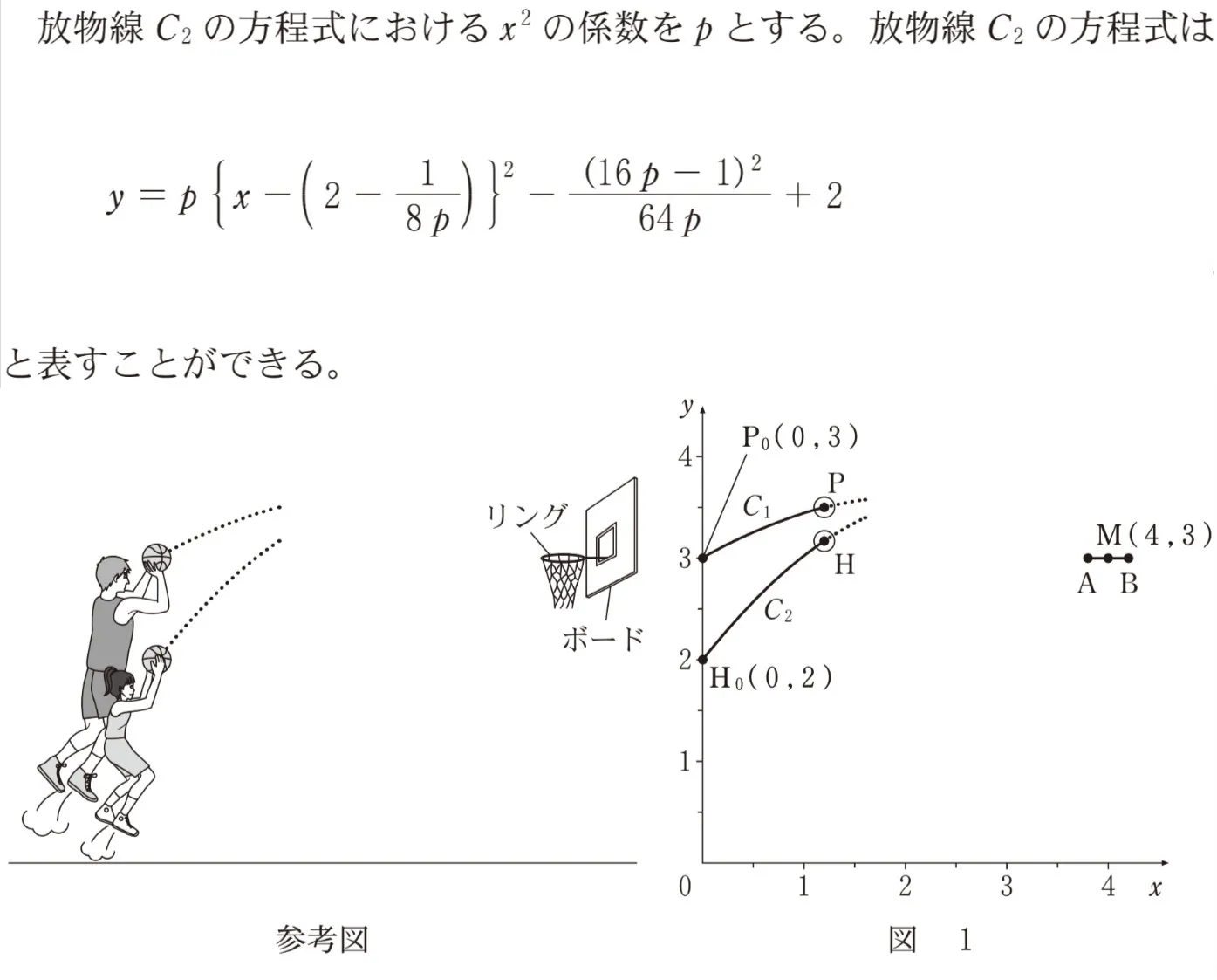
二人は、図1のように座標軸が定められた平面上に、プロ選手と花子さんがシュートを打つ様子を真横から見た図をかき、ボールがリングに入った場合について、後の仮定を設定して考えることにした。長さの単位はメートルであるが、以下では省略する。
＜仮定＞
・平面上では、ボールを直径0.2の円とする。
・リングを真横から見たときの左端を点A（3.8，3）、右端を点B（4.2，3）とし、リングの太さは無視する。
・ボールがリングや他のものに当たらずに上からリングを通り、かつ、ボールの中心がABの中点M（4，3）を通る場合を考える。ただし、ボールがリングに当たるとは、ボールの中心とAまたはBとの距離が0.1以下になることとする。
・プロ選手がシュートを打つ場合のボールの中心を点Pとし、Pは、はじめに点P0（0，3）にあるものとする。また、P0，Mを通る、上に凸の放物線をC1とし、PはC1上を動くものとする。
・花子さんがシュートを打つ場合のボールの中心を点Hとし、Hは、はじめに点H0（0，2）にあるものとする。また、H0，Mを通る、上に凸の放物線をC2とし、HはC2上を動くものとする。
・放物線C1やC2に対して、頂点のy座標を「シュートの高さ」とし、頂点のx座標を「ボールが最も高くなるときの地上の位置」とする。
（1）放物線C1の方程式におけるx2の係数をaとする。放物線C1の方程式は
y＝ax2−（ キ ）ax＋（ ク ）
と表すことができる。また、プロ選手の「シュートの高さ」は
—（ ケ ）a＋（ コ ）
である。
プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」の比較の記述として、正しいものは（ サ ）である。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和5年度（2023年度）本試験 問22（数学Ⅰ・数学A（第2問） 問9） （訂正依頼・報告はこちら）
（ サ ）にあてはまるものを次のうちから1つ選べ。
〔2〕太郎さんと花子さんは、バスケットボールのプロ選手の中には、リングと同じ高さでシュートを打てる人がいることを知り、シュートを打つ高さによってボールの軌道がどう変わるかについて考えている。
二人は、図1のように座標軸が定められた平面上に、プロ選手と花子さんがシュートを打つ様子を真横から見た図をかき、ボールがリングに入った場合について、後の仮定を設定して考えることにした。長さの単位はメートルであるが、以下では省略する。
＜仮定＞
・平面上では、ボールを直径0.2の円とする。
・リングを真横から見たときの左端を点A（3.8，3）、右端を点B（4.2，3）とし、リングの太さは無視する。
・ボールがリングや他のものに当たらずに上からリングを通り、かつ、ボールの中心がABの中点M（4，3）を通る場合を考える。ただし、ボールがリングに当たるとは、ボールの中心とAまたはBとの距離が0.1以下になることとする。
・プロ選手がシュートを打つ場合のボールの中心を点Pとし、Pは、はじめに点P0（0，3）にあるものとする。また、P0，Mを通る、上に凸の放物線をC1とし、PはC1上を動くものとする。
・花子さんがシュートを打つ場合のボールの中心を点Hとし、Hは、はじめに点H0（0，2）にあるものとする。また、H0，Mを通る、上に凸の放物線をC2とし、HはC2上を動くものとする。
・放物線C1やC2に対して、頂点のy座標を「シュートの高さ」とし、頂点のx座標を「ボールが最も高くなるときの地上の位置」とする。
（1）放物線C1の方程式におけるx2の係数をaとする。放物線C1の方程式は
y＝ax2−（ キ ）ax＋（ ク ）
と表すことができる。また、プロ選手の「シュートの高さ」は
—（ ケ ）a＋（ コ ）
である。
プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」の比較の記述として、正しいものは（ サ ）である。
〔2〕太郎さんと花子さんは、バスケットボールのプロ選手の中には、リングと同じ高さでシュートを打てる人がいることを知り、シュートを打つ高さによってボールの軌道がどう変わるかについて考えている。
二人は、図1のように座標軸が定められた平面上に、プロ選手と花子さんがシュートを打つ様子を真横から見た図をかき、ボールがリングに入った場合について、後の仮定を設定して考えることにした。長さの単位はメートルであるが、以下では省略する。
＜仮定＞
・平面上では、ボールを直径0.2の円とする。
・リングを真横から見たときの左端を点A（3.8，3）、右端を点B（4.2，3）とし、リングの太さは無視する。
・ボールがリングや他のものに当たらずに上からリングを通り、かつ、ボールの中心がABの中点M（4，3）を通る場合を考える。ただし、ボールがリングに当たるとは、ボールの中心とAまたはBとの距離が0.1以下になることとする。
・プロ選手がシュートを打つ場合のボールの中心を点Pとし、Pは、はじめに点P0（0，3）にあるものとする。また、P0，Mを通る、上に凸の放物線をC1とし、PはC1上を動くものとする。
・花子さんがシュートを打つ場合のボールの中心を点Hとし、Hは、はじめに点H0（0，2）にあるものとする。また、H0，Mを通る、上に凸の放物線をC2とし、HはC2上を動くものとする。
・放物線C1やC2に対して、頂点のy座標を「シュートの高さ」とし、頂点のx座標を「ボールが最も高くなるときの地上の位置」とする。
（1）放物線C1の方程式におけるx2の係数をaとする。放物線C1の方程式は
y＝ax2−（ キ ）ax＋（ ク ）
と表すことができる。また、プロ選手の「シュートの高さ」は
—（ ケ ）a＋（ コ ）
である。
プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」の比較の記述として、正しいものは（ サ ）である。
- プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」は、つねに一致する。
- プロ選手の「ボールが最も高くなるときの地上の位置」の方が、つねにMのx座標に近い。
- 花子さんの「ボールが最も高くなるときの地上の位置」の方が、つねにMのx座標に近い。
- プロ選手の「ボールが最も高くなるときの地上の位置」の方がMのx座標に近いときもあれば、花子さんの「ボールが最も高くなるときの地上の位置」の方がMのx座標に近いときもある。
正解！素晴らしいです
残念...
この過去問の解説 （2件）
01
問題にある「仮定」の最後の項目から，
プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」は，
それぞれ放物線C1，C2の頂点のx座標です。
前の問題（問21）で，放物線C1の頂点の座標を求めています。
問題文の「仮定」の最後の項目から，
プロ選手の「シュートの高さ」＝放物線C1の頂点のy座標
であることがわかります。
放物線C1の方程式をさらに変形して，
y=a(x2-4x)+3
y=a{(x-2)2-4}+3
y=a(x-2)2-4a+3
よって，放物線C1の頂点の座標は(2,-4a+3)
</blockquote>放物線C1の頂点のx座標は2，すなわち，
プロ選手の「ボールが最も高くなるときの地上の位置」は2で，
Mのx座標は4ですから，その差は2です。
一方，与えられたC2の方程式より，
以上のことから，
花子さんの「ボールが最も高くなるときの地上の位置」の方が、つねにMのx座標に近い。
が正解となります。
正解です。
放物線C2の方程式は問題で与えられているので，
そのまま使いましょう。
式全体を見るとかなりややこしい式に見えますが，
実際にややこしいのは頂点のy座標を表す部分だけで，
頂点のy座標はこの問題では使いません。
重要なのは頂点のx座標と，上に凸であるということです。
参考になった数0
この解説の修正を提案する
02
ボールが最も高くなる位置、つまり軸の位置を比較すれば良いです。
aもpも負の値であることに注意します。
C1, C2の軸はそれぞれ2と2-1/8pです。
軸が大きい値ほど、Mに座標が近いことになります。今、pは上に凸の放物線であることから負の値であることがわかります。
よって 2<2-1/8p であるので、花子さんの方がボールが最も高くなる地上位置がMに近いです。
参考になった数0
この解説の修正を提案する
前の問題（問21）へ
令和5年度（2023年度）本試験 問題一覧
次の問題（問23）へ