大学入学共通テスト(数学) 過去問
令和5年度(2023年度)本試験
問29 (数学Ⅰ・数学A(第3問) 問4)
問題文
<条件>
・それぞれの球を、用意した5色(赤、青、黄、緑、紫)のうちのいずれか1色で塗る。
・1本のひもでつながれた二つの球は異なる色になるようにする。
・同じ色を何回使ってもよく、また使わない色があってもよい。
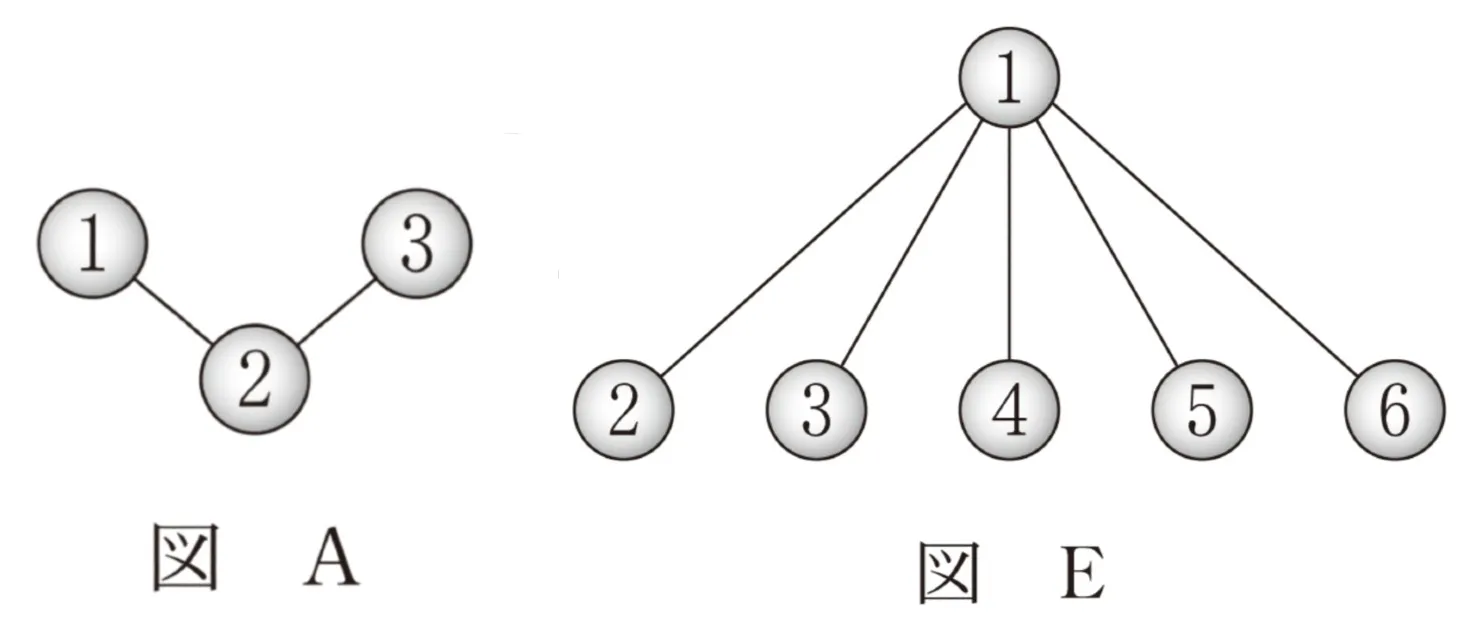
例えば図Aでは、三つの球が2本のひもでつながれている。この三つの球を塗るとき、球1の塗り方が5通りあり、球1を塗った後、球2の塗り方は4通りあり、さらに球3の塗り方は4通りある。したがって、球の塗り方の総数は80である。
(4)図Eにおける球の塗り方のうち、赤をちょうど3回使い、かつ青をちょうど2回使う塗り方は( クケ )通りある。
( クケ )にあてはまるものを次のうちから1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)本試験 問29(数学Ⅰ・数学A(第3問) 問4) (訂正依頼・報告はこちら)
<条件>
・それぞれの球を、用意した5色(赤、青、黄、緑、紫)のうちのいずれか1色で塗る。
・1本のひもでつながれた二つの球は異なる色になるようにする。
・同じ色を何回使ってもよく、また使わない色があってもよい。
例えば図Aでは、三つの球が2本のひもでつながれている。この三つの球を塗るとき、球1の塗り方が5通りあり、球1を塗った後、球2の塗り方は4通りあり、さらに球3の塗り方は4通りある。したがって、球の塗り方の総数は80である。
(4)図Eにおける球の塗り方のうち、赤をちょうど3回使い、かつ青をちょうど2回使う塗り方は( クケ )通りある。
( クケ )にあてはまるものを次のうちから1つ選べ。

- 28
- 30
- 32
- 35
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
球1は他のすべての球とそれぞれ1本のひもでつながれているので,
赤・青以外の色で塗らなければなりません。
よって球1の塗り方は3通りです。
球2~球6の5個は,そのうちのどの2個の球も
1本のひもでつながっていないので,
この5個のうち3個を赤で,2個を青で塗ればよいことになります。
5個の中から青で塗る2個を選び,残り3個を赤で塗ればよいので,
球2~球6の塗り方は5C2=10(通り)
したがって,求める塗り方の総数は
3×10=30(通り)
正解です。
と計算することもできます。
参考になった数0
この解説の修正を提案する
02
赤と青を使う領域を特別なものとして考えましょう。考えてみれば意外とシンプルな問題です。
1番に対して、題意より赤も青も使うことができません。よって3通りの塗り方になります。
残りの5つの球に対し、赤3つと青2つを割り当てるのですが、これはどれも繋がっていないため、自由に組み合わせを決めることができます。
青を塗る2球を決めれば自動的に赤を塗る3球も決まるので、
5C2×3=30通りとなります。
参考になった数0
この解説の修正を提案する
前の問題(問28)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問30)へ