大学入学共通テスト(数学) 過去問
令和5年度(2023年度)本試験
問39 (数学Ⅰ・数学A(第4問) 問7)
問題文
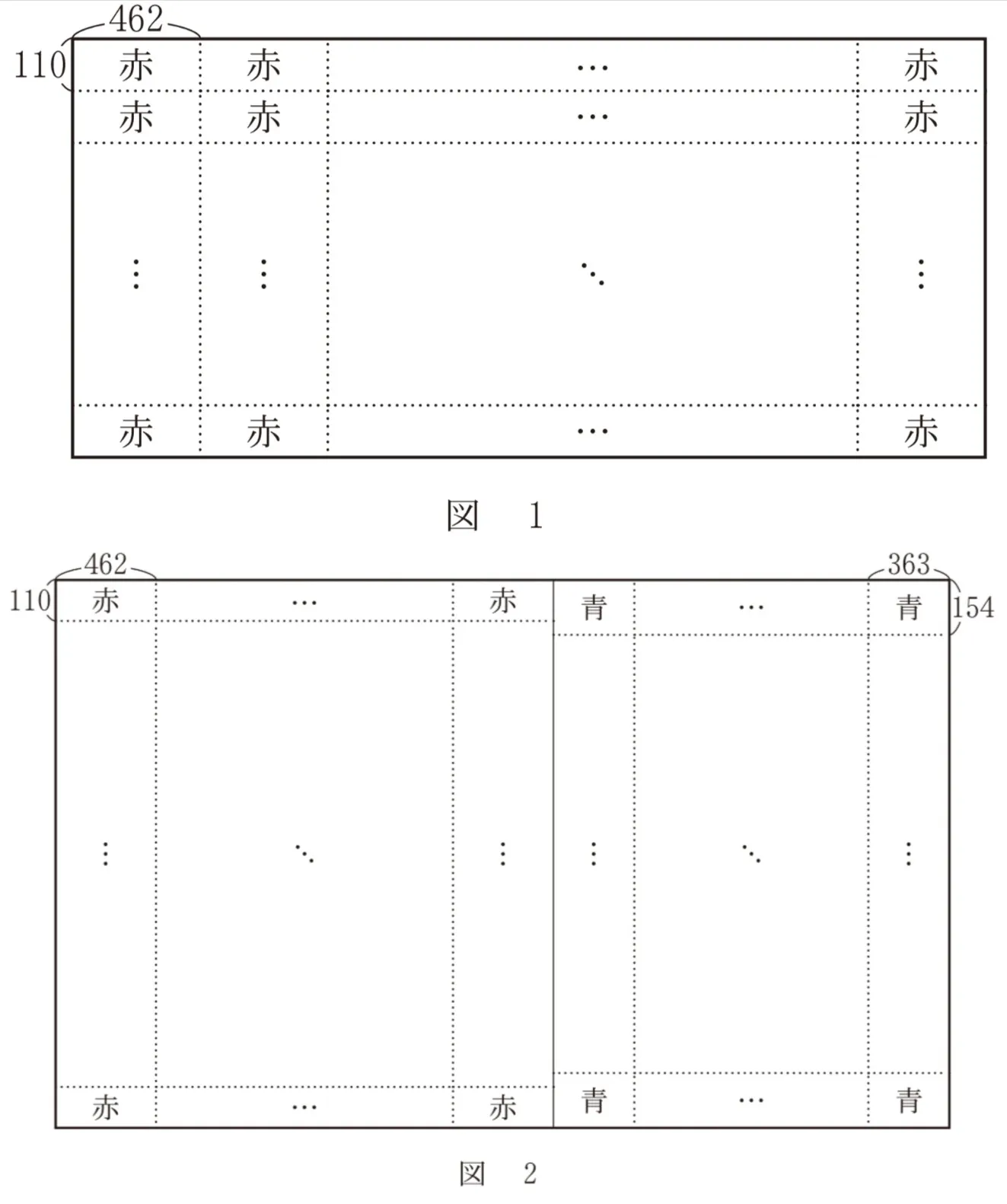
(1)横の長さが462で縦の長さが110である赤い長方形を、図1のように並べて正方形や長方形を作ることを考える。
462と110の両方を割り切る素数のうち最大のものは( アイ )である。
赤い長方形を並べて作ることができる正方形のうち、辺の長さが最小であるものは、一辺の長さが( ウエオカ )のものである。
また、赤い長方形を並べて正方形ではない長方形を作るとき、横の長さと縦の長さの差の絶対値が最小になるのは、462の約数と110の約数を考えると、差の絶対値が( キク )になるときであることがわかる。
縦の長さが横の長さより( キク )長い長方形のうち、横の長さが最小であるものは、横の長さが( ケコサシ )のものである。
(2)花子さんと太郎さんは、(1)で用いた赤い長方形を1枚以上並べて長方形を作り、その右側に横の長さが363で縦の長さが154である青い長方形を1枚以上並べて、図2のような正方形や長方形を作ることを考えている。
このとき、赤い長方形を並べてできる長方形の縦の長さと、青い長方形を並べてできる長方形の縦の長さは等しい。よって、図2のような長方形のうち、縦の長さが最小のものは、縦の長さが( スセソ )のものであり、図2のような長方形は縦の長さが( スセソ )の倍数である。
二人は、次のように話している。
花子:赤い長方形と青い長方形を図のように並べて正方形を作ってみようよ。
太郎:赤い長方形の横の長さが462で青い長方形の横の長さが363だから、図のような正方形の横の長さは462と363を組み合わせて作ることができる長さでないといけないね。
花子:正方形だから、横の長さは( スセソ )の倍数でもないといけないね。
462と363の最大公約数は( タチ )であり、( タチ )の倍数のうちで( スセソ )の倍数でもある最小の正の整数は( ツテトナ )である。
これらのことと、使う長方形の枚数が赤い長方形も青い長方形も1枚以上であることから、図2のような正方形のうち、辺の長さが最小であるものは、一辺の長さが( ニヌネノ )のものであることがわかる。
( ツテトナ )にあてはまるものを次のうちから1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)本試験 問39(数学Ⅰ・数学A(第4問) 問7) (訂正依頼・報告はこちら)
(1)横の長さが462で縦の長さが110である赤い長方形を、図1のように並べて正方形や長方形を作ることを考える。
462と110の両方を割り切る素数のうち最大のものは( アイ )である。
赤い長方形を並べて作ることができる正方形のうち、辺の長さが最小であるものは、一辺の長さが( ウエオカ )のものである。
また、赤い長方形を並べて正方形ではない長方形を作るとき、横の長さと縦の長さの差の絶対値が最小になるのは、462の約数と110の約数を考えると、差の絶対値が( キク )になるときであることがわかる。
縦の長さが横の長さより( キク )長い長方形のうち、横の長さが最小であるものは、横の長さが( ケコサシ )のものである。
(2)花子さんと太郎さんは、(1)で用いた赤い長方形を1枚以上並べて長方形を作り、その右側に横の長さが363で縦の長さが154である青い長方形を1枚以上並べて、図2のような正方形や長方形を作ることを考えている。
このとき、赤い長方形を並べてできる長方形の縦の長さと、青い長方形を並べてできる長方形の縦の長さは等しい。よって、図2のような長方形のうち、縦の長さが最小のものは、縦の長さが( スセソ )のものであり、図2のような長方形は縦の長さが( スセソ )の倍数である。
二人は、次のように話している。
花子:赤い長方形と青い長方形を図のように並べて正方形を作ってみようよ。
太郎:赤い長方形の横の長さが462で青い長方形の横の長さが363だから、図のような正方形の横の長さは462と363を組み合わせて作ることができる長さでないといけないね。
花子:正方形だから、横の長さは( スセソ )の倍数でもないといけないね。
462と363の最大公約数は( タチ )であり、( タチ )の倍数のうちで( スセソ )の倍数でもある最小の正の整数は( ツテトナ )である。
これらのことと、使う長方形の枚数が赤い長方形も青い長方形も1枚以上であることから、図2のような正方形のうち、辺の長さが最小であるものは、一辺の長さが( ニヌネノ )のものであることがわかる。
( ツテトナ )にあてはまるものを次のうちから1つ選べ。

- 2110
- 2210
- 2310
- 2410
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
( スセソ )は問37で,( タチ )は問38でそれぞれ求めました。
( スセソ )は770です。
( タチ )は33です。
この問題では770と33の最小公倍数を求めることになります。
上で引用したように,
770=2×5×7×11
33=3×11
ですから,求める最小公倍数は
2×3×5×7×11=2310
正解です。
( スセソ ),( タチ ),( ツテトナ )と難易度低めの問題が続きますが,
( スセソ ),( タチ )のいずれかを間違えると,( ツテトナ )も,次の( ニヌネノ )も正解できません。
ケアレスミスには十分注意しましょう。
参考になった数0
この解説の修正を提案する
02
問題文から、33と770の最小公倍数を求める問題だと気づきましょう。
aとbの両方の倍数で最小のものとは、最小公倍数のことです。
よって、この問題は33と770の最小公倍数を求める問題です。33=3×11、770=2×5×7×11より、求める最小公倍数は、
2×3×5×7×11=2310となります。
参考になった数0
この解説の修正を提案する
前の問題(問38)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問40)へ