共通テスト（数学） 過去問
令和5年度（2023年度）本試験
問46 (数学Ⅰ・数学A（第5問） 問6)
問題文
（2）円Oに対して、（1）の手順1とは直線lの引き方を変え、次の手順2で作図を行う。
＜手順2＞
（Step1）円Oと共有点をもたない直線lを引く。中心Oから直線lに垂直な直線を引き、直線lとの交点をPとする。
（Step2）円Oの周上に、点Qを∠POQが鈍角となるようにとる。直線PQを引き、円Oとの交点でQとは異なる点をRとする。
（Step3）点Qを通り直線OPに垂直な直線を引き、円Oとの交点でQとは異なる点をSとする。
（Step4）点Sにおける円Oの接線を引き、直線lとの交点をTとする。
このとき、∠PTS＝（ キ ）である。
円Oの半径が√5で、OT＝3√6であったとすると、3点O、P、Rを通る円の半径は
（ ク ）√（ ケ ）／（ コ ）であり、RT＝（ サ ）である。
（ キ ）にあてはまるものを次のうちから1つ選べ。
＜手順2＞
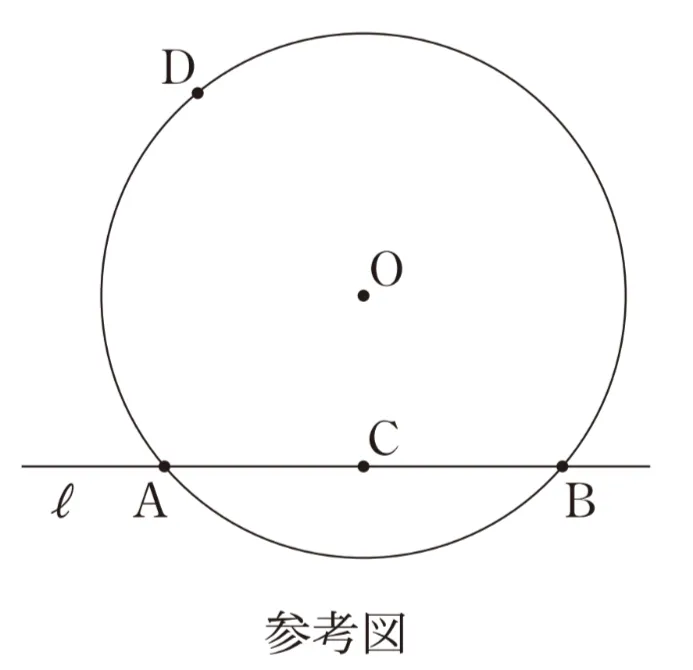
（Step1）円Oと共有点をもたない直線lを引く。中心Oから直線lに垂直な直線を引き、直線lとの交点をPとする。
（Step2）円Oの周上に、点Qを∠POQが鈍角となるようにとる。直線PQを引き、円Oとの交点でQとは異なる点をRとする。
（Step3）点Qを通り直線OPに垂直な直線を引き、円Oとの交点でQとは異なる点をSとする。
（Step4）点Sにおける円Oの接線を引き、直線lとの交点をTとする。
このとき、∠PTS＝（ キ ）である。
円Oの半径が√5で、OT＝3√6であったとすると、3点O、P、Rを通る円の半径は
（ ク ）√（ ケ ）／（ コ ）であり、RT＝（ サ ）である。
（ キ ）にあてはまるものを次のうちから1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
共通テスト（数学）試験 令和5年度（2023年度）本試験 問46（数学Ⅰ・数学A（第5問） 問6） （訂正依頼・報告はこちら）
（2）円Oに対して、（1）の手順1とは直線lの引き方を変え、次の手順2で作図を行う。
＜手順2＞
（Step1）円Oと共有点をもたない直線lを引く。中心Oから直線lに垂直な直線を引き、直線lとの交点をPとする。
（Step2）円Oの周上に、点Qを∠POQが鈍角となるようにとる。直線PQを引き、円Oとの交点でQとは異なる点をRとする。
（Step3）点Qを通り直線OPに垂直な直線を引き、円Oとの交点でQとは異なる点をSとする。
（Step4）点Sにおける円Oの接線を引き、直線lとの交点をTとする。
このとき、∠PTS＝（ キ ）である。
円Oの半径が√5で、OT＝3√6であったとすると、3点O、P、Rを通る円の半径は
（ ク ）√（ ケ ）／（ コ ）であり、RT＝（ サ ）である。
（ キ ）にあてはまるものを次のうちから1つ選べ。
＜手順2＞
（Step1）円Oと共有点をもたない直線lを引く。中心Oから直線lに垂直な直線を引き、直線lとの交点をPとする。
（Step2）円Oの周上に、点Qを∠POQが鈍角となるようにとる。直線PQを引き、円Oとの交点でQとは異なる点をRとする。
（Step3）点Qを通り直線OPに垂直な直線を引き、円Oとの交点でQとは異なる点をSとする。
（Step4）点Sにおける円Oの接線を引き、直線lとの交点をTとする。
このとき、∠PTS＝（ キ ）である。
円Oの半径が√5で、OT＝3√6であったとすると、3点O、P、Rを通る円の半径は
（ ク ）√（ ケ ）／（ コ ）であり、RT＝（ サ ）である。
（ キ ）にあてはまるものを次のうちから1つ選べ。
- ∠PQS
- ∠PST
- ∠QPS
- ∠QRS
- ∠SRT
正解！素晴らしいです
残念...
この過去問の解説 （3件）
01
直線QSと直線OPの交点をUとして
(1)と同様の手順をふむと
∠OST=∠OPT=90° より
四角形OPTSは円に内接するため
∠PTS＝∠UOS=(1/2)∠QOS
円周角の定理から
∠QRS=(1/2)∠QOS
以上より、∠PTS=∠QRS
となります
(１)の直線lが円と2点で交わる位置から円と交点を持たない位置に移動したバージョンと考えます。
E→P
C→R
D→Q
F→U
G→S
T→H
と対応していることをイメージで掴みましょう。
参考になった数0
この解説の修正を提案する
02
直線QSと直線OPの交点をUとします。
（Step1）より，∠OPT＝90°です。
（Step4）より，OSは円Oの半径で直線STは円Oの接線ですから，
∠OST＝90°が成り立ちます。
∠OPT＝∠OST＝90°ですから，
4点O，P，S，Tは線分OTを直径とする同一円周上にあることがわかります。
四角形OPTSは円に内接する四角形ですから，
内角∠PTSと，その対角の外角∠SOUは等しくなります。
すなわち，∠PTS＝∠SOU ……①
①②より
∠PTS＝∠QRS
正解です。
問42～問45がヒントになってこの問題が解きやすくなるように問題が構成されています。
解説を読んでもわかりにくく感じる人は，まず問42～問45の考え方をしっかり理解しましょう。
参考になった数0
この解説の修正を提案する
03
手順にしたがって作図を行い、再び図形の性質を用いて解いていく問題です。
直線OPとQSの交点をUとおきました。
直角と円の接線より、（１）と同様にすると
∠OPT＝∠OST=90°となります。
これより、円周角の定理の逆を用いて、4点O,P,T,Sが一直線上にあることがいえます。
これより、∠PTS＝∠UOSです。
また、円周角の定理（中心角との関係）より、∠UOS=1/2∠QOS=∠QRSであるので、
∠PTS=∠QRSとなります。
参考になった数0
この解説の修正を提案する
前の問題（問45）へ
令和5年度（2023年度）本試験 問題一覧
次の問題（問47）へ