大学入学共通テスト（数学） 過去問
令和5年度（2023年度）本試験
問80 (数学Ⅱ・数学B（第3問） 問2)
問題文
以下の問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。
（1）ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ（単位はg）を表す確率変数をXとする。mとσを正の実数とし、Xは正規分布N（m、σ2）に従うとする。
（ⅰ）この母集団から1個のピーマンを無作為に抽出したとき、重さがmg以上である確率P（X≧m）は
P（X≧m）＝P（X−m／σ≧［ ア ］）＝（ イ／ウ ）
である。
（ イ ）、（ ウ ）にあてはまるものを次のうちから1つ選べ。
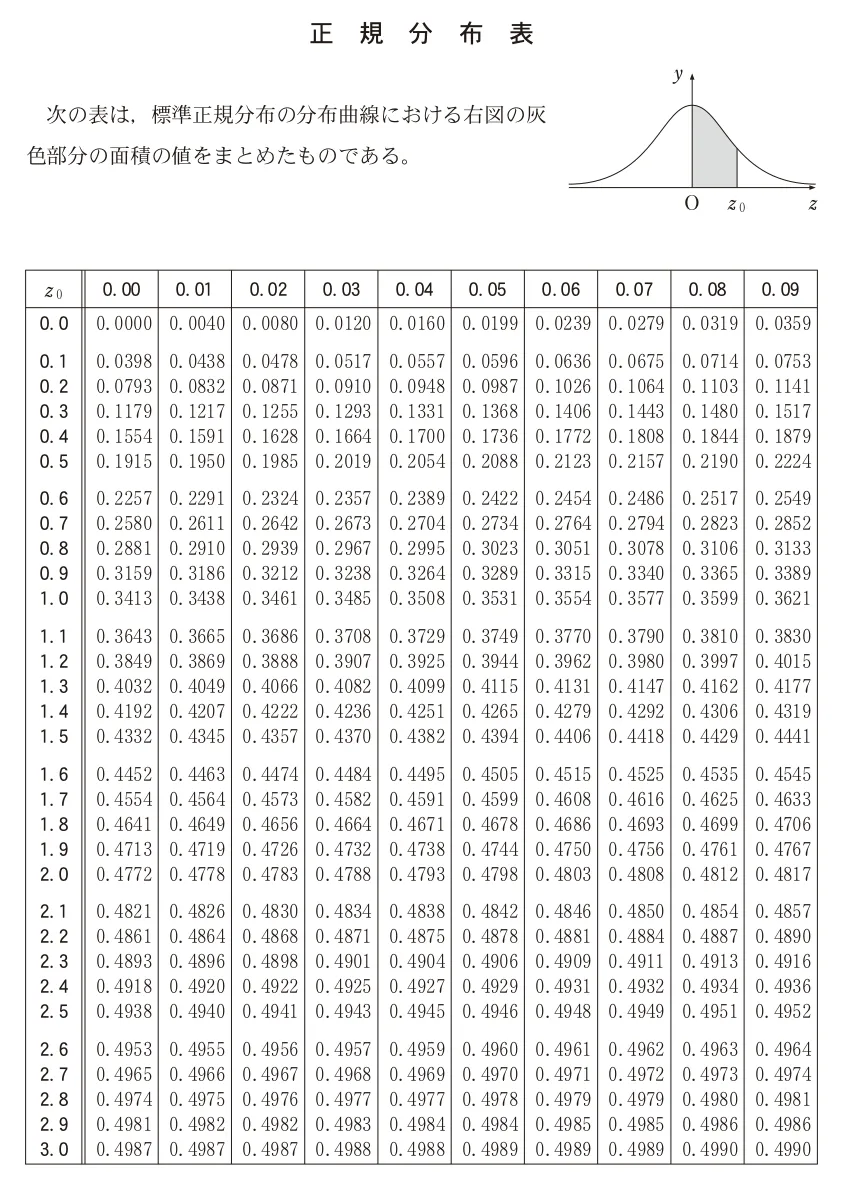
（1）ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ（単位はg）を表す確率変数をXとする。mとσを正の実数とし、Xは正規分布N（m、σ2）に従うとする。
（ⅰ）この母集団から1個のピーマンを無作為に抽出したとき、重さがmg以上である確率P（X≧m）は
P（X≧m）＝P（X−m／σ≧［ ア ］）＝（ イ／ウ ）
である。
（ イ ）、（ ウ ）にあてはまるものを次のうちから1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和5年度（2023年度）本試験 問80（数学Ⅱ・数学B（第3問） 問2） （訂正依頼・報告はこちら）
以下の問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。
（1）ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ（単位はg）を表す確率変数をXとする。mとσを正の実数とし、Xは正規分布N（m、σ2）に従うとする。
（ⅰ）この母集団から1個のピーマンを無作為に抽出したとき、重さがmg以上である確率P（X≧m）は
P（X≧m）＝P（X−m／σ≧［ ア ］）＝（ イ／ウ ）
である。
（ イ ）、（ ウ ）にあてはまるものを次のうちから1つ選べ。
（1）ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ（単位はg）を表す確率変数をXとする。mとσを正の実数とし、Xは正規分布N（m、σ2）に従うとする。
（ⅰ）この母集団から1個のピーマンを無作為に抽出したとき、重さがmg以上である確率P（X≧m）は
P（X≧m）＝P（X−m／σ≧［ ア ］）＝（ イ／ウ ）
である。
（ イ ）、（ ウ ）にあてはまるものを次のうちから1つ選べ。
- イ：1 ウ：2
- イ：2 ウ：2
- イ：2 ウ：3
- イ：3 ウ：3
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
正規分布は平均mを中心に左右対称なので
P(X ≥ m)=1/2
正解です。
参考になった数0
この解説の修正を提案する
前の問題（問79）へ
令和5年度（2023年度）本試験 問題一覧
次の問題（問81）へ