大学入学共通テスト(数学) 過去問
令和6年度(2024年度)本試験
問55 (数学Ⅱ・数学B(第1問) 問4)
問題文
〔1〕(1)k>0、k≠1とする。関数y=logkxとy=log2kxのグラフについて考えよう。
(ⅲ)k=2、3、4のとき
y=logkxのグラフの概形は( カ )
y=log2kxのグラフの概形は( キ )
である。
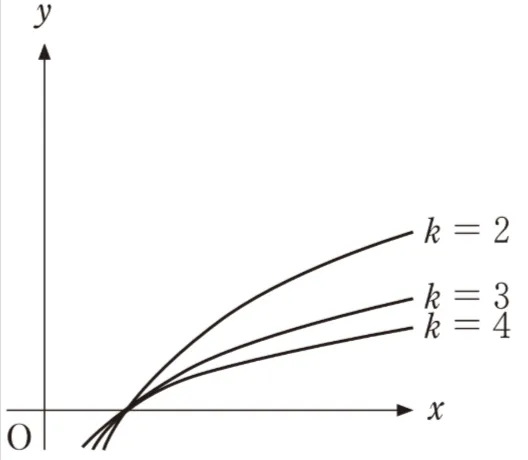
( カ )については、最も適当なものを、次のうちから一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)本試験 問55(数学Ⅱ・数学B(第1問) 問4) (訂正依頼・報告はこちら)
〔1〕(1)k>0、k≠1とする。関数y=logkxとy=log2kxのグラフについて考えよう。
(ⅲ)k=2、3、4のとき
y=logkxのグラフの概形は( カ )
y=log2kxのグラフの概形は( キ )
である。
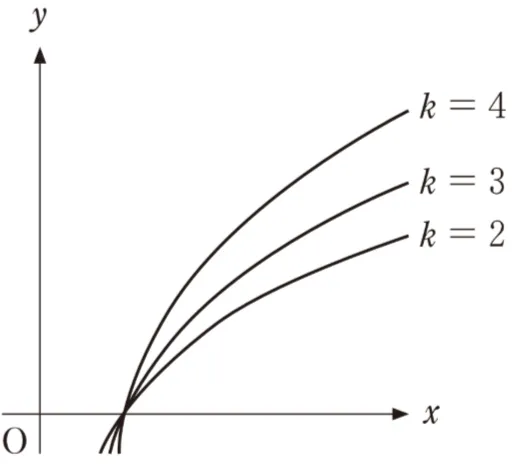
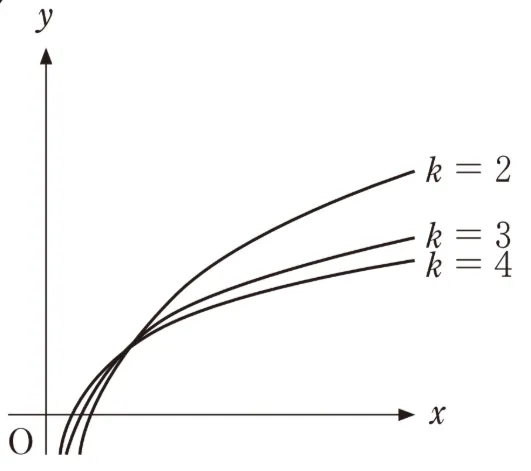
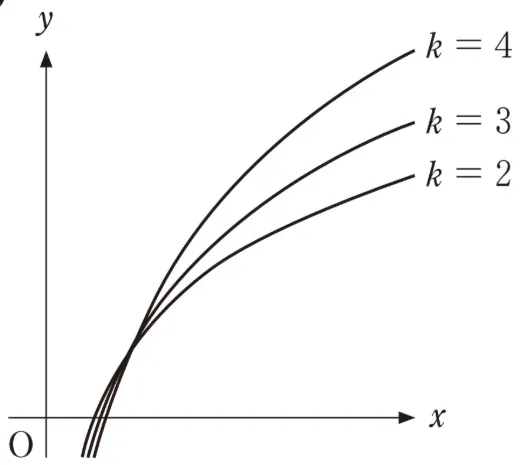
( カ )については、最も適当なものを、次のうちから一つ選べ。
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
まず、対数のグラフは定点(1,0)を通るので、それ以外の選択肢は除外します。
残った選択肢については大小関係を把握したら良い事が分かります。
ここでy=1のときの値を比較します。
(a)k=2のとき
1=log2x
↔x=2
(b)k=3のとき
1=log3x
↔x=3
(c)k=4のとき
1=log4x
↔x=4
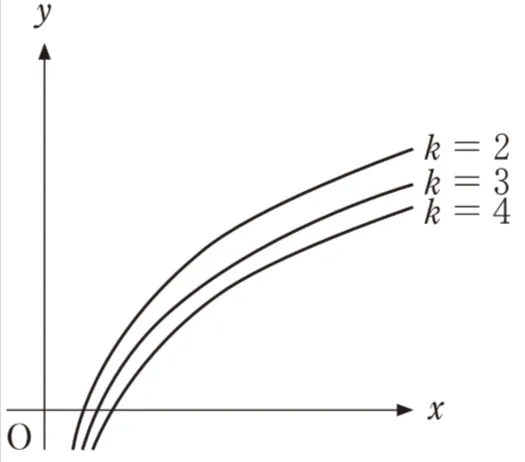
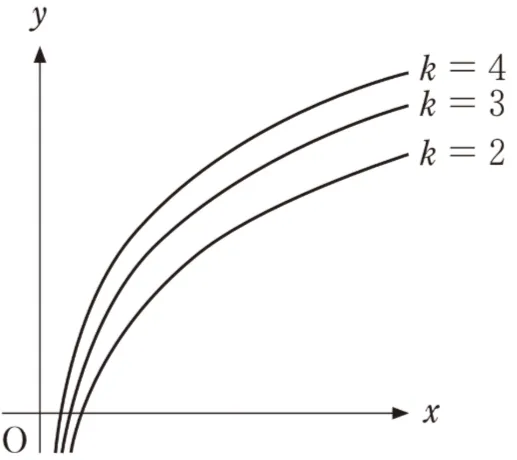
したがって大小関係は(a)<(b)<(c)となります。
上記解説より、この選択肢が正解です。
グラフの関係性を図示できるかがpointとなります。
参考になった数0
この解説の修正を提案する
02
この問題では自然対数をln(k)で表します。
対数関数の微分法を用いると、y=logkxの導関数y'は、
y'=1/(x*ln(k))
となります。
問題の条件よりx>0であり、またkは2,3,4と1より大きい値なのでln(k)>0です。
したがってy'は常に正となり、グラフは増加関数であることが分かります。
ここで、kの値が大きくなるにつれてln(k)の値も大きくなります。
つまりkの値が大きくなるにつれてy'の値は小さくなります。
したがって、kの値が大きくなるほど、x>1の範囲でグラフは接線の傾きが緩やかになることになるため、x軸に近づいていきます。
よって、グラフ全てが点(1,0)を通り、kが大きくなるほどx軸にグラフに近づく図が正解となります。
参考になった数0
この解説の修正を提案する
前の問題(問54)へ
令和6年度(2024年度)本試験 問題一覧
次の問題(問56)へ