大学入学共通テスト（数学） 過去問
令和6年度（2024年度）本試験
問57 (数学Ⅱ・数学B（第1問） 問6)
問題文
〔1〕（2）x＞0、x≠1、y＞0とする。logxyについて考えよう。
（ⅰ）座標平面において、方程式logxy＝2の表す図形を図示すると、（ ク ）のx＞0、x≠1、y＞0の部分となる。
（ ク ）については、最も適当なものを、次のうちから一つ選べ。
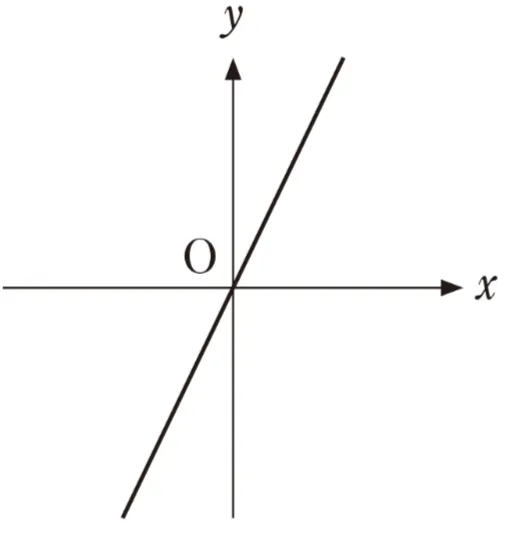
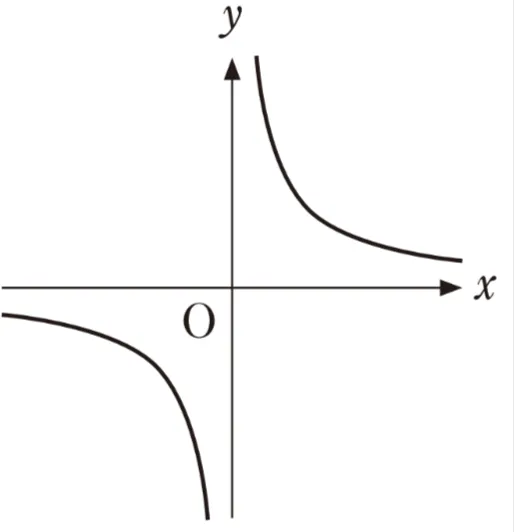
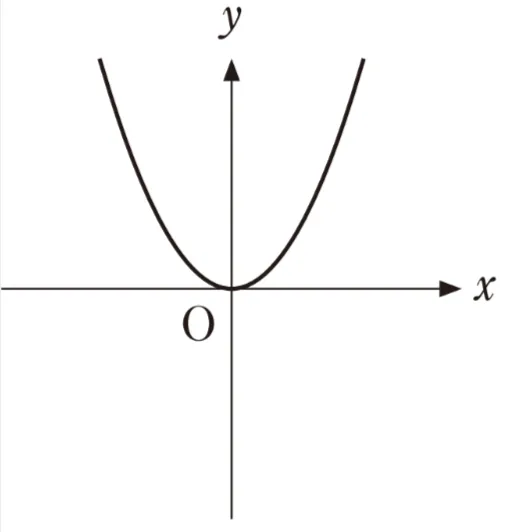
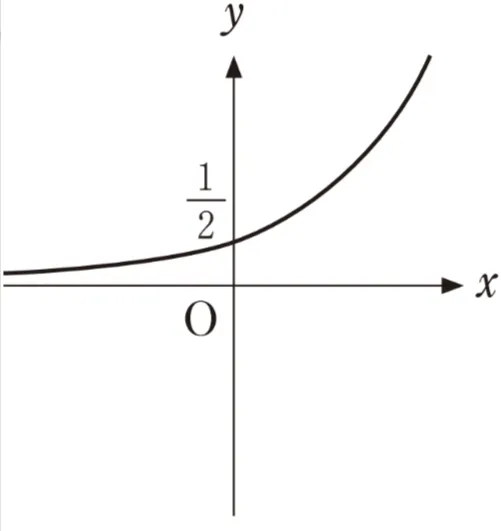
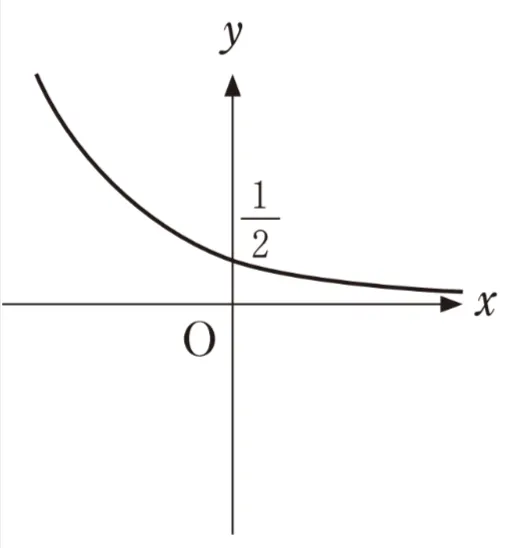
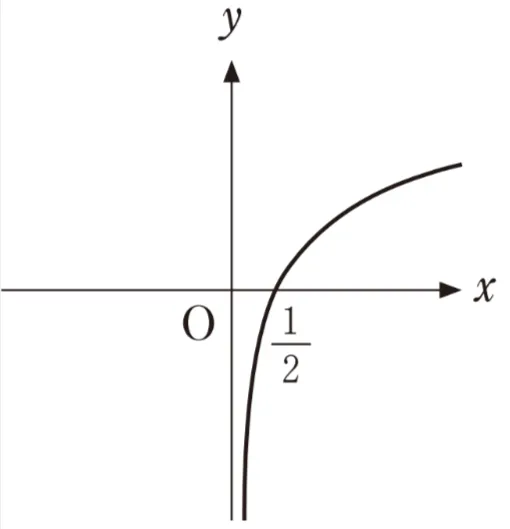
（ⅰ）座標平面において、方程式logxy＝2の表す図形を図示すると、（ ク ）のx＞0、x≠1、y＞0の部分となる。
（ ク ）については、最も適当なものを、次のうちから一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和6年度（2024年度）本試験 問57（数学Ⅱ・数学B（第1問） 問6） （訂正依頼・報告はこちら）
〔1〕（2）x＞0、x≠1、y＞0とする。logxyについて考えよう。
（ⅰ）座標平面において、方程式logxy＝2の表す図形を図示すると、（ ク ）のx＞0、x≠1、y＞0の部分となる。
（ ク ）については、最も適当なものを、次のうちから一つ選べ。
（ⅰ）座標平面において、方程式logxy＝2の表す図形を図示すると、（ ク ）のx＞0、x≠1、y＞0の部分となる。
（ ク ）については、最も適当なものを、次のうちから一つ選べ。
正解！素晴らしいです
残念...
この過去問の解説 （2件）
01
logxy＝2は指数・対数の関係性より
y=x2と表すことができます。
上記解説より、この選択肢が正解です。
指数・対数の関係性を復習しておくことが大切です。
参考になった数0
この解説の修正を提案する
02
対数の定義より、logxy=2はx2=yと書き換えることができます。
問題文よりx>0、x≠1、y>0です。
まず、y=x2という関係式において、x>0であれば、y>0となります。
よって、考えるべき条件はx>0とx≠1です。
したがって、方程式logxy=2が表す図形は、
放物線y=x2のグラフのうち、x>0の部分から、x=1の点である(1,1)を除いたものとなります。
参考になった数0
この解説の修正を提案する
前の問題（問56）へ
令和6年度（2024年度）本試験 問題一覧
次の問題（問58）へ