大学入学共通テスト（数学） 過去問
令和6年度（2024年度）本試験
問82 (数学Ⅱ・数学B（第2問） 問14)
問題文
（ テ ）にあてはまるものを1つ選べ。 
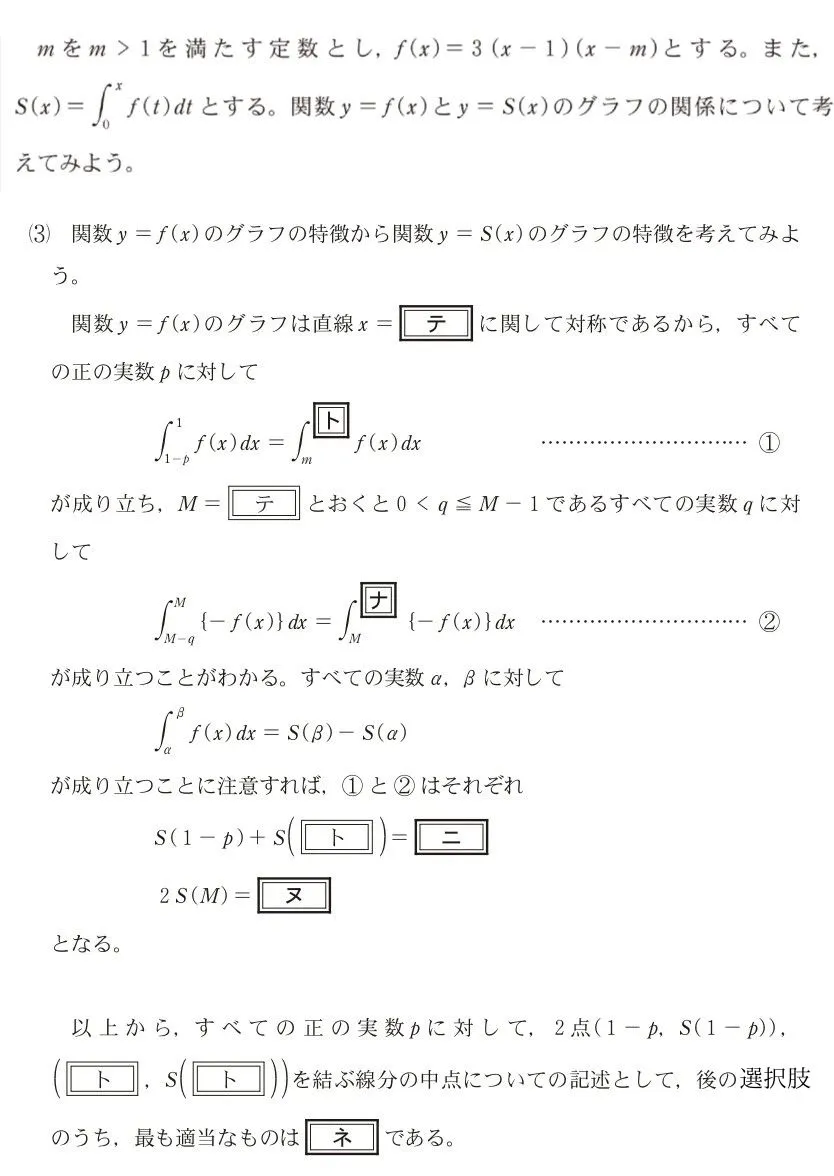
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和6年度（2024年度）本試験 問82（数学Ⅱ・数学B（第2問） 問14） （訂正依頼・報告はこちら）
（ テ ）にあてはまるものを1つ選べ。
- m
- m／2
- m＋1
- （m＋1）／2
正解！素晴らしいです
残念...
この過去問の解説 （2件）
01
y=f(x)を展開すると
y=3(x-1)(x-m)
=3(x2-(m+1)x+m)
=3(x-(m+1)/2)2-((m+1)/2)2+m)
従って、x=(m+1)/2に関して対称なグラフとなります。
正解です。
グラフの特徴からとあるので、どういうグラフになるか推定できる状態にすることが大切です。
参考になった数0
この解説の修正を提案する
02
f(x)はx=1,mでx軸と交わる２次関数です。
よってこの中点を通るy軸に並行な直線に関して対象です。
つまりテは(m+1)/2
参考になった数0
この解説の修正を提案する
前の問題（問81）へ
令和6年度（2024年度）本試験 問題一覧
次の問題（問83）へ