大学入学共通テスト(数学) 過去問
令和6年度(2024年度)本試験
問87 (数学Ⅱ・数学B(第2問) 問19)
問題文
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
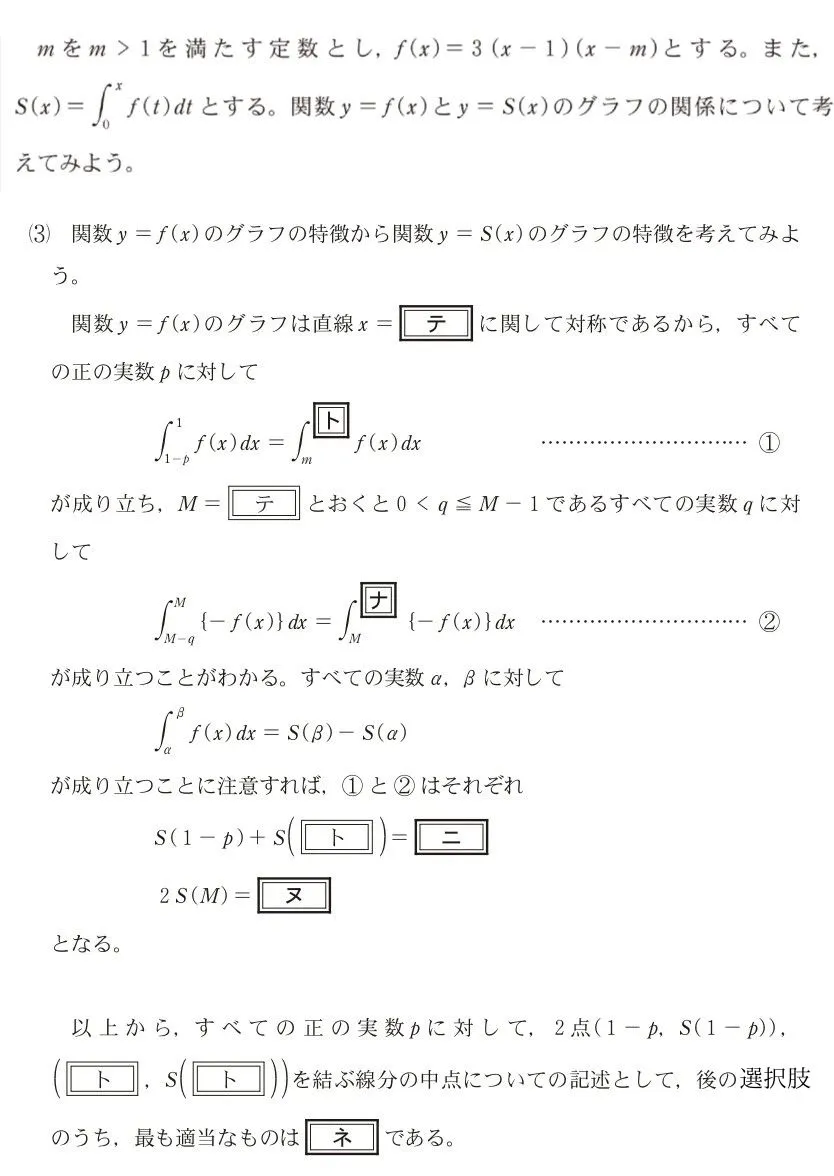
大学入学共通テスト(数学)試験 令和6年度(2024年度)本試験 問87(数学Ⅱ・数学B(第2問) 問19) (訂正依頼・報告はこちら)

- x座標はpの値によらず一つに定まり、y座標はpの値により変わる。
- x座標はpの値により変わり、y座標はpの値によらず一つに定まる。
- 中点はpの値によらず一つに定まり、関数y=S(x)のグラフ上にある。
- 中点はpの値によらず一つに定まり、関数y=f(x)のグラフ上にある。
- 中点はpの値によって動くが、つねに関数y=S(x)のグラフ上にある。
- 中点はpの値によって動くが、つねに関数y=f(x)のグラフ上にある。
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
y=f(x)を展開すると
y=3(x-1)(x-m)
=3(x2-(m+1)x+m)
=3(x-(m+1)/2)2-((m+1)/2)2+m)
従って、x=(m+1)/2に関して対称なグラフとなります。
該当範囲を図示すると下図の薄赤部のようになるから、対称な範囲は濃赤部となります。
従って、トにはm+pが入ります。
該当範囲を図示すると下図の薄青部のようになるから、対称な範囲は濃青部となります。
従って、中点はpの値によらず一つに定まり、関数y=S(x)のグラフ上にあることが分かります。
正解です。
中点に関する記述があるため各点を算出し、前問をうまく用いて整理していくことが大切です。
参考になった数0
この解説の修正を提案する
02
まず下の方程式を用意します。
S(1)+S(m)=S(1-p)+S(m+p)
2S(M)=S(M-q)+S(M+q)
さらに条件からq=M-1とします。
さて、中点を求めていきましょう。
(S(1-p)+S(m+p))/2=(S(1)+S(m))/2
=(S(1)+S(2M-1))/2
=(S(M-q)+S(M+q))/2
=S(M)
(1-p+m+p)/2=(1+m)/2=M
よって中点は(M,S(M))とわかります。
答えは、中点はpの値によって決まらず、
y=S(x)上にあると言えます。
参考になった数0
この解説の修正を提案する
前の問題(問86)へ
令和6年度(2024年度)本試験 問題一覧
次の問題(問88)へ