大学入学共通テスト（数学） 過去問
令和6年度（2024年度）本試験
問91 (数学Ⅱ・数学B（第3問） 問4)
問題文
（ エ ）にあてはまるものを1つ選べ。
以下の問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。また、ここでの晴れの定義については、気象庁の天気概況の「快晴」または「晴」とする。
（1）太郎さんは、自分が住んでいる地域において、日曜日に晴れとなる確率を考えている。
晴れの場合は1、晴れ以外の場合は0の値をとる確率変数をXと定義する。また、X＝1である確率をpとすると、その確率分布は表1のようになる。
以下の問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。また、ここでの晴れの定義については、気象庁の天気概況の「快晴」または「晴」とする。
（1）太郎さんは、自分が住んでいる地域において、日曜日に晴れとなる確率を考えている。
晴れの場合は1、晴れ以外の場合は0の値をとる確率変数をXと定義する。また、X＝1である確率をpとすると、その確率分布は表1のようになる。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和6年度（2024年度）本試験 問91（数学Ⅱ・数学B（第3問） 問4） （訂正依頼・報告はこちら）
（ エ ）にあてはまるものを1つ選べ。
以下の問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。また、ここでの晴れの定義については、気象庁の天気概況の「快晴」または「晴」とする。
（1）太郎さんは、自分が住んでいる地域において、日曜日に晴れとなる確率を考えている。
晴れの場合は1、晴れ以外の場合は0の値をとる確率変数をXと定義する。また、X＝1である確率をpとすると、その確率分布は表1のようになる。
以下の問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。また、ここでの晴れの定義については、気象庁の天気概況の「快晴」または「晴」とする。
（1）太郎さんは、自分が住んでいる地域において、日曜日に晴れとなる確率を考えている。
晴れの場合は1、晴れ以外の場合は0の値をとる確率変数をXと定義する。また、X＝1である確率をpとすると、その確率分布は表1のようになる。
正解！素晴らしいです
残念...
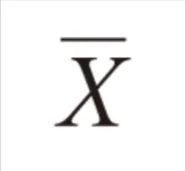
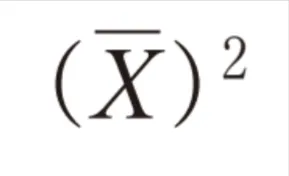
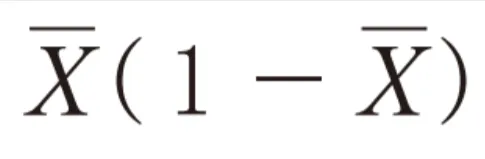
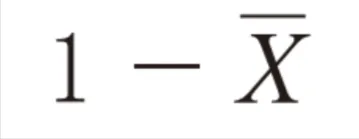
この過去問の解説 （2件）
01
期待値mは
m=(1-p)・0+p・1=p
n=300は十分に大きいと考えられるため
正規分布N(m,σ2/n)
と表せられます。
正解です。
題意より代入して整理することで算出できます。
参考になった数0
この解説の修正を提案する
02
Xi2 = Xi (i=1,...,n)を代入します。
(X12+...+Xn2)/n-X2=(1-X)X
参考になった数0
この解説の修正を提案する
前の問題（問90）へ
令和6年度（2024年度）本試験 問題一覧
次の問題（問92）へ